Hogyan kell beilleszteni a matematikai képleteket a webhelyen?

Ha valaha is hozzá kell adnod egy vagy két matematikai képletet egy weboldalon, akkor ez a legkönnyebben megteheti, amint azt a cikkben leírtuk: a matematikai képletek könnyen beilleszthetők a webhelybe, olyan képek formájában, amelyek automatikusan generálják az alfa volfrámat. Az egyszerűség mellett ez az egyetemes módon javíthatja a webhely láthatóságát a keresőmotorokban. Hosszú ideig működik (és azt hiszem, örökre fog működni), de erkölcsileg elavult.

Ha folyamatosan használja a matematikai képleteket a webhelyén, azt javaslom, hogy használja a Mathjax-ot - egy speciális JavaScript könyvtárat, amely matematikai megnevezést jelenít meg a Mathml, Latex vagy Asciimathml jelölés használatával.

Kétféle módon kezdi el használni MathJax: (1) A rendszer segítségével egy egyszerű kód, akkor gyorsan csatlakoztathatja a MathJax script, hogy a webhely, ami automatikusan automatikusan betölti a távoli szerverről a kívánt on; (2) Töltse le a Mathjax parancsfájlt egy távoli kiszolgálóról a kiszolgálóra, és csatlakoztassa a webhely összes oldalához. A második módszer sokkal bonyolultabb és hosszabb - felgyorsítja a letöltési az oldalt a webhely, és ha a szülő MathJax szerver valamilyen okból elérhetetlenné válik, ez nem befolyásolja a saját honlapján. Ezen előnyök ellenére az első módot választottam egyszerűbb, gyors és nem igényel technikai készségeket. Kövesse a példát, és 5 perc múlva használhatja a Mathjax összes funkcióját a webhelyén.

A Mathjax Library parancsfájlt a távoli kiszolgálóról két kód opcióval, a Mathjax fő webhelyén vagy a Dokumentációs oldalon készítheti el:

Az egyik kódolási lehetőséget át kell másolni, és helyezze be a weboldal kódja, lehetőleg a címkék között és Vagy közvetlenül a címke után . Az első verzió szerint a Mathjax gyorsabban van betöltve és lassítja az oldalt. De a második lehetőség automatikusan nyomon követi és betölti a legújabb Mathjax verziókat. Ha behelyezi az első kódot, akkor rendszeres időközönként frissíteni kell. Ha behelyezi a második kódot, az oldalak lassabbak lesznek, de nem kell folyamatosan felügyelni a Mathjax frissítéseket.

Connect Mathjax a legegyszerűbb módja a Bloggernek vagy a Wordpressnek: adjunk hozzá egy widget egy harmadik féltől származó JavaScript kód beillesztéséhez, hogy beillesszék a fent bemutatott letöltési kód első vagy második verzióját, és helyezzük közelebb a widgetet a sablon elejéhez (az úton , ez egyáltalán nem szükséges, mivel a mathjax szkript aszinkron módon van betöltve). Ez minden. Most olvassa el a Mathml, Latex és Asciimathml Markup szintaxist, és készen áll a matematikai képletek beszúrására a webhely weboldalain.

Bármely fraktál egy olyan konkrét szabályon alapul, amelyet következetesen korlátlan számú alkalommal alkalmaz. Mindenkit megöntöznek.

Az iteratív algoritmus a menühöz szivacs elkészítéséhez meglehetősen egyszerű: az 1. oldalú forráskocka az arcával párhuzamos síkokkal van osztva, 27 egyenlő kockával. Egy központi kocka és 6 szomszédos kocka eltávolításra kerül. A 20 hátralévő kisebb kockát tartalmazó készletet kapjuk. Azáltal, hogy mindegyik kocka mindegyikével egy készletet kapunk, amely már 400 kisebb kockából áll. A folyamat folytatása végtelenül, menges szivacsot kapunk.

www.syt. Lehetővé teszi, hogy megtalálja. A webhely kiszámítást eredményez. Néhány másodpercig a kiszolgáló megadja a helyes döntést. Jellemző egyenlet a mátrixhoz lesz egy algebrai kifejezés, amely a meghatározó számítási szabály szerint található matriák matriákUgyanakkor a fő átlósok lesznek a különbség az átlós elemek és a változó értékei között. Kiszámításkor jellemző egyenlet az online mátrixhoz, Minden elem matriák megszorozzák a megfelelő többi elemet matriák. Keresse meg az üzemmódot online csak a téren lehet matriák. Műveleti megállapítás jellemző egyenlet az online mátrixhoz az elemek termékének algebrai mennyiségének kiszámításához jön le matriák Ennek eredményeként meghatározó matriák, csak meghatározás céljából jellemző egyenlet az online mátrixhoz. Ez a művelet egy különleges helyet foglal el az elméletben mátrixLehetővé teszi, hogy saját számokat és vektorokat találjon gyökerekkel. Feladat a megállapításhoz jellemző egyenlet az online mátrixhoz az elemek megszorítása matriák Ezeknek a munkálatoknak a későbbi összegzésével egy adott szabály szerint. www.syt. kitalál a mátrix jellemzési egyenlete meghatározott méretű módban online. Számítás jellemző egyenlet az online mátrixhoz Egy adott dimenzióval a numerikus vagy szimbolikus együtthatókkal rendelkező polinom megtalálása a determináns kiszámításának megfelelően matriák - a megfelelő elemek munkáinak összege matriák, csak meghatározás céljából jellemző egyenlet az online mátrixhoz. A polinom a négyzet alakú változóhoz képest matriákMint meghatározás jellemző egyenlet a mátrixhozElosztott elméletben mátrix. A polinom gyökereinek értéke jellemző egyenlet az online mátrixhoz Saját vektorok és sajátértékek meghatározására használják matriák. Ugyanakkor, ha a meghatározó matriák akkor nulla lesz a mátrix jellemző egyenlete még mindig létezik, ellentétben a fordítva matriák. A kiszámításához a mátrix jellemzési egyenlete vagy azonnal találjon azonnal mátrixok jellemző egyenletek, nem kell kevesebb időt és erőfeszítést költeni, míg a szerverünk másodpercek alatt megtalálja. a mátrix online jellemzési egyenlete. Ebben az esetben a válasz megtalálható jellemző egyenlet az online mátrixhoz helyes és megfelelő pontossággal lesz, még akkor is, ha a számok vannak jellemző egyenlet az online mátrixhoz Irracionális lesz. Online www.syt. A szimbolikus rekordok megengedettek az elemekben. mátrix, én a mátrix online jellemzési egyenlete számításkor általános szimbólum formájában lehet bemutatni jellemző egyenletmátrix online. Hasznos a megállapítás feladatainak megoldása során kapott válasz ellenőrzésére jellemző egyenlet az online mátrixhozA webhely használata www.syt.. Polinomiális számítási művelet végrehajtásakor - a mátrix jellemző egyenleteEz a feladat megoldásakor figyelni és rendkívül koncentrálni kell. A honlapunk segíti Önt a témáról. jellemző egyenletmátrix online. Ha nincs ideje a hosszú ellenőrzések megoldására, akkor www.syt. biztosan kényelmes eszköz lesz az ellenőrzéshez, amikor megtalálja és kiszámítja jellemző egyenlet az online mátrixhoz.

Saját értékek (számok) és sajátvektorok.
Példák megoldásokra

Légy önmagad

Mindkét egyenletből következik, hogy.

Tedd, akkor: .

Ennek eredményeként: - A második saját vektor.

Megismételjük a döntés fontos pontjait:

- a keletkező rendszer természetesen általános megoldással rendelkezik (egyenletek lineárisan függő);

- "Igarek" Kiválasztjuk, hogy ez az egész és az első "uncia" koordináta - az egész, pozitív és a lehető legkisebb.

- Ellenőrizzük, hogy a privát megoldás megfelel-e minden rendszeregyenletnek.

Válasz .

A közbülső "vezérlési pontok" meglehetősen elegendő volt, így az egyenlőtlenségek vizsgálata elvileg túlzottabb.

Különböző információforrások esetén a saját vektorok koordinátáit gyakran nem oszlopokban rögzítik, hanem húrokban, például: (és őszintén szólva, én magam is használtam őket sorok szerint). Ez az opció elfogadható, de a téma fényében lineáris transzformációk Kényelmesebb használni technikailag vektoros oszlopok.

Talán az oldat nagyon hosszúnak tűnt neked, de ez csak azért van, mert kommentáltam nagyon részletesen az első példát.

2. példa.

Matriák

Tanítjuk magad! A követelés tervezési feladatának példakénti mintája a lecke végén.

Néha további feladatot kell végrehajtania, nevezetesen:

Írjon egy kanonikus bomlást a mátrixról

Ami?

Ha saját mátrix vektorai formájában alapul, akkor ő fog képviselni az űrlapon:

Ahol - a saját vektorok koordinátáiból álló mátrix - Átlós Mátrix megfelelő saját számokkal.

A mátrix bomlását hívják kánoni vagy Átlós.

Tekintsük az első példa mátrixát. Saját vektorai lineárisan független (NonollyLinear) és alapul. Mátrixot készítsen koordinátáikból:

A fő átlós Matriák a megfelelő sorrendben Saját számok találhatók, és a fennmaradó elemek nulla:
- Ismét hangsúlyozom a megrendelés fontosságát: "Két" megfelel az 1. vektornak, és az 1. oszlopban található, "trojka" - 2. vektor.

A megállapítás szokásos algoritmusánál fordított mátrix vagy gaussa-Jordániamegtalálja . Nem, ez nem egy hibás! - Ritka, mint napfogyatkozás esemény, amikor a fordított egybeesett az eredeti mátrixdal.

Továbbra is rögzíti a mátrix kanonikus bomlását:

A rendszer megoldható elemi átalakításokkal és a következő példákban, amelyek ezt a módszert alkalmazzuk. De itt sokkal gyorsabban működik "iskola". A 3. egyenletből kifejezünk: - a második egyenlet helyettesítése:

Mivel az első koordináta nulla, megkapjuk a rendszert, mindegyik egyenletből, hogy következik.

És újra figyeljen a lineáris függőség kötelező jelenlétére. Ha csak triviális megoldást kapunk , Vagy a saját szám helytelenül megtalálható, vagy a hiba elkészítése / megoldása a rendszer.

A kompakt koordináták értéket adnak

EIGenVector:

És ismét - ellenőrizze, hogy a megoldás megtalálható-e kielégíti az egyes rendszeregyenlést. A későbbi bekezdésekben és a későbbi feladatokban javaslom, hogy elfogadja ezt a kívánságot a kötelező szabályt.

2) A saját értéke ugyanazon az elven kapjuk a következő rendszert:

A rendszer második egyenletét, kifejezjük: - a harmadik egyenlet helyettesítése:

Mivel a "Zetovaya" koordináta nulla, megkapjuk a rendszert minden olyan egyenletből, amely lineáris függőségnek kell lennie.

Legyen

Ellenőrizze, hogy a döntés Megfelel az egyes rendszeregyenleteknek.

Így saját vektor :.

3) és végül a rendszer megfelel saját értéküknek:

A második egyenlet a legkönnyebben néz ki, ezért kifejezjük és helyettesítjük az 1. és 3. egyenletben:

Minden jól látható - egy lineáris függőség kiderült, amelyet a kifejezésben helyettesítünk:

Az "x" és az "igrek" eredményeként a Zeta-n keresztül fejeződött be :. A gyakorlatban nem szükséges az ilyen összefüggések elérése, egyes esetekben kényelmesebb az expressz és a via. Vagy akár egy "vonat" - például "x" keresztül az "igrek", és "igrek" a "zet" -on keresztül

Tedd, akkor:

Ellenőrizze, hogy a megoldás megtalálható-e megfelel az egyes rendszeregyenleteknek, és írja a harmadik sajátvektorot

Válasz: Saját vektorok:

Geometrikusan ezek a vektorok három különböző térbeli irányt állítanak fel ("Oda és vissza")amelyekre lineáris transzformáció Transzfer nem nulla vektorok (sajátvektorok) a kollineáris vektorokhoz.

Ha az állapot alatt meg kellett találni egy kanonikus bomlást, akkor itt lehetséges, mert A különböző természetes számok megfelelnek a különböző lineárisan független sajátvektoroknak. Mátrix készítése koordinátáikból, átlós mátrixból nak,-nek ide vonatkozó Saját értékek és találatok fordított mátrix .

Ha a feltöltendő állapotban rögzítené lineáris konverziós mátrix a sajátvektorok bázisában, Adom a választ az űrlapon. Van egy különbség, és a különbség elengedhetetlen! Mert ez egy mátrix - van egy "de" mátrix.

Feladat egyszerűbb számítástechnikával az önálló döntésekhez:

5. példa.

Keresse meg a saját lineáris konverziós vektorokat a mátrix által megadott

A saját számok megtalálásakor ne próbálja meg, hogy ne hozza az ügyet a 3. fokozat polinomjához. Ezenkívül a rendszer megoldásai eltérhetnek az én megoldásaimtól - nincs egyértelműség; És a vektorok, amelyeket meg fog találni, eltérhet a minta vektoroktól a megfelelő koordináták arányosságának pontosságával. Például, és. Esztétikusan válaszoljon a formában, de semmi szörnyű, ha megáll és a második verzióban. Mindazonáltal minden ésszerű határérték, a verzió már nem nagyon jó.

Példamutató tiszta minta tervezése a feladat végén a lecke.

Hogyan oldja meg a feladatot több őshonos szám esetén?

Az általános algoritmus ugyanaz marad, de itt vannak saját jellemzői, és a megoldás egyes szakaszai tanácsosak abban, hogy ellenálljanak a szigorúbb tudományos stílusban:

6. példa.

Keressen saját számokat és saját vektorokat

Döntés

Természetesen megszakítom a mesés első oszlopot:

És a négyzet háromszoros bomlása után a szorzókhoz:

Ennek eredményeképpen eigenvalues-t kaptunk, amelyek közül kettő többszörös.

Megtaláljuk saját vektorainkat:

1) magányos katonával, egy "egyszerűsített" sémára oszlik:

Az utolsó két egyenletből az egyenlőség jól látható, amely nyilvánvalóan a rendszer 1. egyenletébe kell helyettesítenie:

A legjobb kombináció nem talál:
EIGenVector:

2-3) Most távolítsa el néhány órát. Ebben az esetben kiderülhet kettő vagy egy sajátvektor. A gyökerek sokasága ellenére helyettesítjük a meghatározó értéket Ki hoz minket a következőkre a lineáris egyenletek homogén rendszere:

A saját vektorok pontosan vektorok
alapvető rendszer megoldások

Valójában az egész leckében csak azzal foglalkozunk azzal, hogy az alapvető rendszer vektorai voltak. Csak addig, amíg ez a kifejezés nem volt különösebbre. By the way, azok az okos diákok, akik Maskhalatsban elcsúszották a témát homogén egyenletekkénytelen lesz ugrani most.

Az egyetlen művelet a felesleges vonalak eltávolítása volt. Ennek eredményeképpen az "egy-három" mátrix a közepén formális "lépéssel" kapható.
- Alapváltozó, - Ingyenes változók. Két szabad változó tehát az alaprendszer vektorai is két.

Az alapváltozót ingyenes változókon keresztül fejezze ki :. Az "xom" előtti nulla tényező lehetővé teszi, hogy teljesen bármilyen értéket (ami jól látható az egyenletek rendszeréből).

E feladat összefüggésében az általános megoldás kényelmesebb, hogy ne írja le a karakterláncban, hanem az oszlopban:

A pár megfelel a saját vektorának:
A pár megfelel a saját vektorának:

jegyzet : A kifinomult olvasók kiválaszthatják ezeket a vektorokat és orálisan - csak elemezni a rendszert De itt van szükségünk néhány tudásra: változók - három, rank Matrix rendszer - egységeszköz alapvető megoldások rendszere 3 - 1 \u003d 2 vektorból áll. Azonban a látható vektorok kiválóan láthatóak, és ezeknek a tudásnak anélkül, hogy ezek a tudás tisztán intuitív szinten van. Ugyanakkor a harmadik vektort még akkor is rögzítjük :. Azonban figyelmeztetés, egy másik példa szerint egy egyszerű kiválasztás nem lehet, ezért a foglalás a tapasztalt emberek számára készült. Ezen kívül, miért ne vegye figyelembe a harmadik vektor, mondd ,? Végtére is, a koordinátái szintén megfelelnek az egyes rendszerek egyenletének és vektoroknak lineárisan független. Ez az opció elvben alkalmas, de "ívelt", mivel a "másik" vektor az alaprendszer vektorai lineáris kombinációja.

Válasz: Saját számok:, Saját vektorok:

Hasonló példa az önmegoldásokra:

7. példa.

Keressen saját számokat és saját vektorokat

Példamutató minta kialakítás a lecke végén.

Meg kell jegyezni, hogy a 6. és 7. példában három lineárisan önálló sajátvektort kapunk, ezért a kezdeti mátrixot kanonikus bomlásban mutatjuk be. De az ilyen málna nem minden esetben történik:

8. példa.

Döntés: Töltse fel és oldja meg a jellemző egyenletet:

Az első oszlop feltárásával határozza meg:

További egyszerűsítéseket végeznek a figyelembe vett módszer szerint, elkerülve a polinom 3. fokozatot:

- Saját jelentések.

Megtaláljuk saját vektorainkat:

1) A nehézségek gyökerével nem fordul elő:

Ne meglepődjenek, a beállított készlet mellett változók is változók - nincs különbség.

A 3. egyenletek közül kifejezünk - az 1. és 2. egyenletben helyettesítjük:

Mindkét egyenletből következik:

Hagyja, majd:

2-3) Több értékre kapjuk a rendszert .

A rendszermátrixot és az elemi átalakítások segítségével írjuk meg, hogy egy lépésképpen adjuk meg:

Homogén lineáris egyenletek rendszere

A homogén lineáris egyenletek rendszerét a nézetrendszernek nevezik

Nyilvánvaló, hogy ebben az esetben mivel Az egyes oszlopok összes eleme ezeken a meghatározókban nulla.

Mivel az ismeretlenek a formulákon vannak , akkor az esetben, ha Δ ≠ 0, a rendszernek egyetlen nulla megoldása van x. = y. = z. \u003d 0. Számos feladatban azonban a kérdés, hogy egy homogén megoldási rendszer eltérjen a nullától.

Tétel. Annak érdekében, hogy a lineáris homogén egyenletek rendszere nem nulla megoldás legyen, szükséges, és elegendő δ ≠ 0.

Tehát, ha a determináns δ ≠ 0, akkor a rendszer egyetlen megoldással rendelkezik. Ha Δ ≠ 0, akkor a lineáris homogén egyenletek rendszere végtelen több megoldás.

Példák.

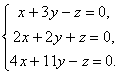
Saját vektorok és mátrix Eigenvalues

Hagyja adni egy négyzetes mátrixot , X. - néhány mátrix oszlop, amelynek magassága egybeesik a mátrix sorrendjével A.. .

Sok feladatnak meg kell fontolnia az egyenletet X.

ahol λ szám. Nyilvánvaló, hogy bármilyen λ esetében ez az egyenlet nulla megoldást tartalmaz.

A λ szám, amelyben ez az egyenlet nem nulla megoldásokat tartalmaz, hívják saját jelentése Matriák A., de X. Ezzel a λ -val saját vektor Matriák A..

Keresse meg saját vektor mátrixát A.. Amennyiben E.∙X \u003d X., akkor a mátrixegyenlet újraírható, mint vagy . Expandált formában ez az egyenlet átírható, mint egy lineáris egyenletek rendszere. Igazán .

És ezért,

Tehát kaptunk egy homogén lineáris egyenleteket a koordináták meghatározásához x 1, x 2, x 3. Vektor X.. Annak érdekében, hogy a rendszer nem nulla megoldásokat kapjon, elegendő ahhoz, hogy a rendszer determináns legyen nulla, azaz.

Ez az egyenlet a λ-hoz viszonyítva 3. fokozat. Ezt hívják jellegzetes egyenlet Matriák A. és a saját értékeinek meghatározására szolgál.

Minden Eigenvalue λ megfelel saját vektorának X.amelynek koordinátáit a rendszerből a λ megfelelő értékével határozzák meg.

Példák.

Vektor algebra. Egy vektor fogalma

A fizika különböző szakaszainak tanulmányozásakor az értékek megtalálhatók, amelyeket teljes mértékben meghatároznak numerikus értékeik, például hossz, terület, tömeg, hőmérséklet stb. Az ilyen értékeket skalárnak nevezik. Azonban azonban olyan értékek is, amelyek meghatározzák, hogy a numerikus érték mellett is meg kell ismerni az irányt az űrben, például a testen működő erő, a test sebessége és gyorsulása Amikor az űrben mozog, a mágneses mező feszültsége ezen a ponton és stb. Az ilyen értékeket vektornak nevezik.

Szigorú definíciót vezetünk be.

Irányított vágás Felhívjuk a szegmenst, amelyhez a végeihez képest ismert, hogy melyik az első, és melyik a második.

Vektor úgynevezett irányított szegmens, amelynek határozott hossza, vagyis Ez egy bizonyos hosszúságú szegmens, amely az egyik korlátozó pontja az elejére történik, és a második a végére. Ha egy A. - a vektor kezdete B. - A vége, akkor a vektort a szimbólum jelöli, ráadásul a vektort gyakran egy betű jelzi. Az ábrán a vektort egy szegmens jelöli, és iránya nyílja.

Modul vagy lena A vektort az irányított szegmens hosszának nevezik. Jelöli || vagy ||.

A vektorokhoz az úgynevezett nulla vektort is tulajdonítjuk, amely a kezdet és a vég egybeesik. Ez jelzi. A nulla vektor nincs bizonyos iránya, és modulja nulla || \u003d 0.

Vektorok és hívják kollekorHa egy egyenes vonalon vagy párhuzamos egyenes vonalon találhatók. Ugyanakkor, ha a vektorok egyformán irányulnak, írunk, ellentétesek.

Az azonos síkkal párhuzamos egyenes vonalon található vektorok hívják bonyolult.

Két vektorot hívnak egyenlőHa ezek a kollekorok, egyformán irányulnak és egyenlőek. Ebben az esetben írnak.

A vektorok egyenlőségének meghatározását követően következik, hogy a vektort párhuzamosan át lehet adni magával, úgy, hogy kezdete a hely bármely pontjáról.

például.

Lineáris műveletek a vektorok felett

1. A vektor számát.

   A vektor termékét a λ számra új vektornak nevezik, hogy:

   A vektor termékét a λ számon jelöljük.

   

   Például, Van egy vektor, amely ugyanolyan oldalra irányul, mint egy vektor, és hossza kétszer olyan kisebb, mint a vektor.

   A bevezetett művelet a következő tulajdonságok:

2. Vektorok hozzáadása.

   Legyen mindkettő két önkényes vektor. Tegyen önkényes pontot O. És építsen egy vektort. A pont után A. Vektort írunk. Az első vektor kezdetét összekötő vektor a második végével hívják összeg Ezek a vektorok és jelzik .

   

   A beágyazott vektorok hívásának megfogalmazott meghatározása parallográfia szabályaMivel ugyanolyan mennyiségű vektorok érhetők el az alábbiak szerint. Elhalasztja a pontot O. Vektorok és. Építsd ezeket a vektorokat Parallelogrammok Ouks.. A vektorok óta, akkor egy vektor, a felső párhuzamos párhuzamos átlója O.nyilvánvaló lesz a vektorok összege.

   

   Könnyen ellenőrizze az alábbiakat vektorok hozzáadásának tulajdonságai.

3. Vektor különbség.

   Vektor, Collinear ebben a vektorban, egyenlő neki hosszú és ellentétesen irányított, hívott szemben Vektor a vektorhoz és kijelölt. Az ellenkező vektor a vektor sokszorosításának eredményeként tekinthető a λ \u003d -1 :.