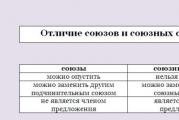
Keresse meg a lineáris operátor sajátértékeit, amelyeket egy mátrix ad meg. A mátrix jellegzetes egyenlete
Hogyan lehet beágyazni a matematikai képleteket egy weboldalra?
Ha valaha is hozzá kell adnia egy vagy két matematikai képletet egy weboldalhoz, akkor ennek legegyszerűbb módja a cikkben leírtak szerint: matematikai képletek könnyen beilleszthetők az oldalra olyan képek formájában, amelyeket a Wolfram Alpha automatikusan generál. Az egyszerűség mellett ez a sokoldalú módszer javítja webhelye láthatóságát a keresőkben. Hosszú ideje működik (és azt hiszem, örökké fog működni), de erkölcsileg már elavult.
Ha rendszeresen használ matematikai képleteket a webhelyén, akkor javasoljuk, hogy használja a MathJax-ot, egy speciális JavaScript-könyvtárat, amely a matematikai jelöléseket megjeleníti a webböngészőkben a MathML, a LaTeX vagy az ASCIIMathML jelöléssel.
A MathJax használatának megkezdésének kétféle módja van: (1) egy egyszerű kód használatával gyorsan összekapcsolhat egy MathJax parancsfájlt a webhelyével, amelyet a megfelelő időben automatikusan betölt egy távoli szerverről (szerverlista); (2) töltse fel a MathJax parancsfájlt egy távoli szerverről a szerverére, és csatlakoztassa azt a webhely minden oldalához. A második, bonyolultabb és időigényesebb módszer felgyorsítja webhelye oldalainak betöltését, és ha a szülő MathJax szerver valamilyen okból átmenetileg elérhetetlenné válik, ez semmilyen módon nem érinti a saját webhelyét. Ezen előnyök ellenére az első módszert választottam, mivel egyszerűbb, gyorsabb és nem igényel technikai ismereteket. Kövesse példámat, és 5 perc múlva képes lesz használni a weboldal összes MathJax funkcióját.
Csatlakoztathatja a MathJax könyvtár szkriptjét egy távoli szerverről a kód két verziójával a MathJax fő webhelyéről vagy a dokumentációs oldalról:
Ezen kódváltozatok egyikét át kell másolni és be kell illeszteni a weboldal kódjába, lehetőleg a címkék közé
és vagy közvetlenül a címke után ... Az első lehetőség szerint a MathJax gyorsabban töltődik be, és kevésbé lassítja az oldalt. De a második lehetőség automatikusan követi és betölti a MathJax legújabb verzióit. Ha behelyezi az első kódot, akkor azt rendszeresen frissíteni kell. Ha behelyezi a második kódot, az oldalak lassabban töltődnek be, de nem kell folyamatosan figyelnie a MathJax frissítéseit.A MathJax összekapcsolásának legegyszerűbb módja a Blogger vagy a WordPress: a webhely irányítópultján adjon hozzá egy modult harmadik féltől származó JavaScript-kód beillesztéséhez, másolja bele a fenti betöltőkód első vagy második verzióját, és helyezze közelebb a widgetet a sablon elejéhez (egyébként ez egyáltalán nem szükséges mert a MathJax szkript aszinkron módon van betöltve). Ez minden. Most ismerje meg a MathML, a LaTeX és az ASCIIMathML jelölési szintaxist, és készen áll a matematikai képletek beágyazására a webhelye weboldalaira.
Bármely fraktál egy bizonyos szabály szerint épül fel, amelyet egymás után korlátlan számú alkalommal alkalmaznak. Minden ilyen időpontot iterációnak nevezünk.
A Menger szivacs elkészítéséhez szükséges iteratív algoritmus meglehetősen egyszerű: az eredeti oldalsó kockát az 1. oldalával az arcával párhuzamos síkok osztják 27 egyenlő kockára. Egy központi kockát és 6 szomszédos kockát távolítunk el belőle. Kiderül egy készlet, amely 20 megmaradt kisebb kockából áll. Ugyanezzel a lépéssel mindegyik kockával kapunk egy készletet, amely már 400 kisebb kockából áll. Ezt a folyamatot végtelenül folytatva kapunk egy Menger szivacsot.
www.hely segítségével megtalálhatja. A helyszín elvégzi a számítást. Néhány másodperc múlva a szerver megadja a helyes megoldást. A mátrix jellemző egyenlete algebrai kifejezés lesz, amelyet a determináns kiszámításához a szabály talál meg mátrixok mátrixok, míg a fő átló a különbség az átlós elemek és a változó között lesz. Számításkor a mátrix karakterisztikus egyenletének online, minden elem mátrixok szaporodni fog a megfelelő egyéb elemekkel mátrixok... Keresés módban online csak négyzetre lehetséges mátrixok... Keresse meg a műveletet a mátrix karakterisztikus egyenletének online az elemek szorzatának algebrai összegének kiszámításához redukálódik mátrixok a meghatározó megtalálása eredményeként mátrixok, csak annak meghatározása céljából a mátrix karakterisztikus egyenletének online... Ez a művelet elméletben különleges helyet foglal el. mátrixok, lehetővé teszi sajátértékek és vektorok megtalálását gyökerek felhasználásával. A megtalálás feladata a mátrix karakterisztikus egyenletének online az elemek szaporítása mátrixok e művek későbbi összegzésével egy bizonyos szabály szerint. www.hely megtalálja a mátrixra jellemző egyenlet adott dimenzió a módban online... Számítás a mátrix karakterisztikus egyenletének online egy adott dimenzióhoz numerikus vagy szimbolikus együtthatójú polinomot talál, amelyet a determináns kiszámításának szabálya szerint talál mátrixok - a megfelelő elemek szorzatának összegeként mátrixok, csak annak meghatározása céljából a mátrix karakterisztikus egyenletének online... Polinom keresése egy négyzet változójában mátrixokdefinícióként a mátrixra jellemző egyenlet, elméletben gyakori mátrixok... A polinom gyökereinek értéke a mátrix karakterisztikus egyenletének online a sajátvektorok és sajátértékek meghatározására szolgál mátrixok... Sőt, ha a meghatározó mátrixok akkor nulla lesz mátrix karakterisztikus egyenlete továbbra is léteznek, ellentétben a fordítottal mátrixok... Számítás céljából a mátrixra jellemző egyenlet vagy keressen egyszerre többet mátrixok jellegzetes egyenletei, sok időt és erőfeszítést kell eltölteni, miközben szerverünk megtalálja az online mátrix jellemző egyenlete... Sőt, a válasz az, hogy megtalálja a mátrix karakterisztikus egyenletének online helyes és kellő pontosságú lesz, még akkor is, ha a számokat megtalálja a mátrix karakterisztikus egyenletének online irracionális lesz. Az oldalon www.hely karakter bejegyzések megengedettek az elemekben mátrixokazaz az online mátrix jellemző egyenlete kiszámításakor általános szimbolikus formában ábrázolható a mátrix jellemző egyenlete online... Hasznos ellenőrizni a kapott választ a megtalálás problémájának megoldása során a mátrix karakterisztikus egyenletének onlineaz oldal használata www.hely... A polinom számításának végrehajtásakor - a mátrix jellegzetes egyenlete, figyelmesnek és rendkívül koncentráltnak kell lennie a probléma megoldása során. Viszont webhelyünk segít ellenőrizni a témával kapcsolatos döntését online mátrix karakterisztikus egyenlet... Ha nincs ideje a megoldott problémák hosszú ellenőrzésére, akkor www.hely kétségtelenül kényelmes eszköz lesz az ellenőrzéshez a keresés és a számítás során a mátrix karakterisztikus egyenletének online.
Sajátértékek (számok) és sajátvektorok.
Megoldási példák
Légy önmagad
Mindkét egyenletből az következik.
Tegyük fel akkor: ![]() .
.
Ennek eredményeként: ![]() A második sajátvektor.
A második sajátvektor.
Ismételjük meg a megoldás fontos pontjait:
- a kapott rendszernek minden bizonnyal van általános megoldása (az egyenletek lineárisan függenek);
- úgy választjuk meg a "játékot", hogy egész legyen, és az első "x" koordináta egész, pozitív és a lehető legkisebb legyen.
- ellenőrizze, hogy az adott megoldás kielégíti-e a rendszer egyes egyenleteit.
Válasz ![]() .
.
Volt elég elég köztes "ellenőrző pont", ezért az egyenlőség ellenőrzése elvileg felesleges.
Különböző információforrásokban a sajátvektorok koordinátáit gyakran nem oszlopokba, hanem sorokba írják, például: ![]() (és őszintén szólva magam is szoktam sorokba írni)... Ez a lehetőség elfogadható, de a téma fényében lineáris transzformációk technikailag kényelmesebb használni oszlopvektorok.
(és őszintén szólva magam is szoktam sorokba írni)... Ez a lehetőség elfogadható, de a téma fényében lineáris transzformációk technikailag kényelmesebb használni oszlopvektorok.
Talán a megoldás nagyon hosszúnak tűnt az Ön számára, de ez csak azért van, mert az első példát nagyon részletesen kommentáltam.
2. példa
Mátrixok
Képezzük magunkat! Körülbelüli példa a feladat befejezésére az óra végén.
Néha további feladatra van szükség, nevezetesen:
írja meg a kanonikus mátrixbontást
Ami?
Ha a mátrix sajátvektorai kialakulnak alapján, akkor a következőképpen ábrázolható:
Hol van a sajátvektorok koordinátáiból álló mátrix, - átlós mátrix megfelelő sajátértékekkel.
Ilyen mátrixbontást nevezünk kánoni vagy átlós.
Tekintsük az első példa mátrixát. Saját vektorai ![]() lineárisan független (nem kollináris) és alapot képeznek. Készítsünk egy mátrixot a koordinátáikból:
lineárisan független (nem kollináris) és alapot képeznek. Készítsünk egy mátrixot a koordinátáikból:
![]()
A főátló mátrixok a megfelelő sorrendben a sajátértékek találhatók, és a többi elem egyenlő nulla:
- még egyszer hangsúlyozom a sorrend fontosságát: a "kettő" megfelel az 1. vektornak, ezért az 1. oszlopban található, a "három" - a 2. vektornak.
A megtalálás szokásos algoritmusa szerint inverz mátrix vagy gauss-Jordan módszermegtalálja ![]() ... Nem, ez nem elírás! - előtted ritka esemény, például napfogyatkozás, amikor az inverz egybeesik az eredeti mátrixszal.
... Nem, ez nem elírás! - előtted ritka esemény, például napfogyatkozás, amikor az inverz egybeesik az eredeti mátrixszal.
Marad a mátrix kanonikus lebontásának leírása: ![]()

A rendszer elemi transzformációk segítségével megoldható és a következő példákban ezt a módszert fogjuk használni. De itt az "iskola" módszer sokkal gyorsabban működik. A 3. egyenletből kifejezzük: - a második egyenletben helyettesítjük: 
Mivel az első koordináta nulla, kapunk egy rendszert, amelynek minden egyenletéből ez következik.
És újra figyeljen a lineáris függőség kötelező jelenlétére... Ha csak triviális megoldást kap ![]() , akkor vagy hibásan találták meg a sajátértéket, vagy a rendszert hibával fordították / oldották meg.
, akkor vagy hibásan találták meg a sajátértéket, vagy a rendszert hibával fordították / oldották meg.
A kompakt koordináták jelentést adnak
Sajátvektor: 
És még egyszer - ellenőrizzük a megtalált megoldást ![]() kielégíti a rendszer minden egyenletét... A következő bekezdésekben és a későbbi feladatokban azt javaslom, hogy ezt a kívánságot vegye kötelező szabálynak.
kielégíti a rendszer minden egyenletét... A következő bekezdésekben és a későbbi feladatokban azt javaslom, hogy ezt a kívánságot vegye kötelező szabálynak.
2) A sajátértékre ugyanazon elv szerint a következő rendszert kapjuk: 
A rendszer 2. egyenletéből kifejezzük: - a harmadik egyenletben helyettesítsük: 
Mivel a "zeta" koordináta nulla, kapunk egy rendszert, amelynek minden egyenletéből lineáris függőség következik.
Legyen ![]()
Ellenőrizzük, hogy a megoldás ![]() kielégíti a rendszer minden egyenletét.
kielégíti a rendszer minden egyenletét.
Így a sajátvektor :.
3) És végül a rendszer megfelel a sajátértéknek: 
A második egyenlet a legegyszerűbbnek tűnik, ezért kifejezzük belőle, és behelyettesítjük az 1. és a 3. egyenletre:
![]()
Minden jó - lineáris kapcsolat alakult ki, amelyet helyettesítünk a kifejezésben:
Ennek eredményeként az "x" és az "igrek" kifejezéseket "z" -en keresztül fejezték ki:. A gyakorlatban nem szükséges csak ilyen kapcsolatokat elérni, egyes esetekben kényelmesebb kifejezni mind keresztül, mind azon keresztül. Vagy akár egy "vonat" - például "X" az "igrek" -ig és az "igrek" az "z" -ig
Akkor tegyük fel:
Ellenőrizzük, hogy a megtalált megoldás-e ![]() kielégíti a rendszer minden egyenletét, és leírja a harmadik sajátvektort
kielégíti a rendszer minden egyenletét, és leírja a harmadik sajátvektort
Válasz: sajátvektorok: 
Geometriai szempontból ezek a vektorok három különböző térbeli irányt határoznak meg ("Oda és vissza")amellyel lineáris transzformáció átalakítja a nem nulla vektorokat (sajátvektorokat) a hozzájuk kollináris vektorokká.
Ha a feltétel szükséges egy kanonikus bontás megtalálásához, akkor ez itt lehetséges, mivel a különböző sajátértékek megfelelnek a különböző, lineárisan független sajátvektoroknak. A mátrix összeállítása  koordinátáikból az átlós mátrix
koordinátáikból az átlós mátrix  nak,-nek a megfelelő sajátértékek és megtalálja inverz mátrix .
nak,-nek a megfelelő sajátértékek és megtalálja inverz mátrix .
Ha feltétel szerint írnod \u200b\u200bkell lineáris transzformáció mátrixa a sajátvektorok alapján, akkor a választ formában adjuk meg. Van különbség, és a különbség jelentős! Ugyanis ez a mátrix a „de” mátrix.
Probléma egyszerűbb számításokkal egy független megoldáshoz:
5. példa
Keresse meg a mátrix által adott lineáris transzformáció sajátvektorait! 
Amikor megtalálja a sajátértékeket, próbáljon ne a 3. fokú polinomra kerülni. Ezenkívül a rendszermegoldásai eltérhetnek az én megoldásaimtól - itt nincs egyértelműség; és a megtalált vektorok eltérhetnek a mintavektoroktól a megfelelő koordináták arányosságáig. Például és. Esztétikusabb a választ formában bemutatni, de nem baj, ha a második lehetőségnél áll meg. Mindennek azonban vannak ésszerű korlátai, a verzió már nem nagyon néz ki.
A feladat hozzávetőleges végső mintája a lecke végén.
Hogyan lehet megoldani a problémát több sajátérték esetén?
Az általános algoritmus változatlan, de megvannak a maga sajátosságai, és tanácsos a megoldás egyes részeit szigorúbb tudományos stílusban fenntartani:
6. példa
Keresse meg a sajátértékeket és a sajátvektorokat 
Döntés
Természetesen a mesés első oszlopot nagybetűvel írjuk: 
És a négyzet alakú trinomiális faktorálás után:
Ennek eredményeként sajátértékeket kapunk, amelyek közül kettő többszörös.
Keressük meg a sajátvektorokat:
1) A magányos katonával az "egyszerűsített" rendszer szerint foglalkozunk:

Az utolsó két egyenletből jól látható az egyenlőség, amelyet nyilvánvalóan helyettesíteni kell a rendszer 1. egyenletével:
Nincs jobb kombináció:
Sajátvektor:
2-3) Most lőj pár őrséget. Ebben az esetben kiderülhet akár kettő, akár egy sajátvektor. A gyökerek sokaságától függetlenül az értéket a determinánssal helyettesítjük  ami a következőket hozza elénk homogén lineáris egyenletrendszer:
ami a következőket hozza elénk homogén lineáris egyenletrendszer:
A sajátvektorok pontosan vektorok
alapvető döntési rendszer
Valójában az egész lecke során csak az alaprendszer vektorainak felkutatásával foglalkoztunk. Csak egyelőre erre a kifejezésre nem volt különösebben szükség. Egyébként azok az okos diákok, akik álcakabátban csúsztatták a témát homogén egyenletekmost meg kell ennie.

Az egyetlen lépés az extra sorok eltávolítása volt. Az eredmény egy-három mátrix, amelynek közepén formális "rung" van.
- alapváltozó, - szabad változók. Két szabad változó létezik, ezért az alaprendszer vektorai szintén kettő.
Fejezzük ki az alapváltozót szabad változókkal: Az "x" előtti nulla tényező lehetővé teszi, hogy abszolút bármilyen értéket vegyen fel (ami jól látható az egyenletrendszerből).
E probléma összefüggésében kényelmesebb az általános megoldást nem sorban, hanem oszlopban írni:
A párnak saját vektora van:
A párnak saját vektora van:
jegyzet
: A kifinomult olvasók fel tudják venni ezeket a vektorokat és szóban is - csak a rendszer elemzésével  , de itt némi ismeretre van szükség: három változó létezik, rendszermátrix rang - egység, ami azt jelenti alapvető döntési rendszer 3 - 1 \u003d 2 vektorból áll. A talált vektorok azonban ezen ismeretek nélkül is tökéletesen láthatók, pusztán intuitív szinten. Ebben az esetben a harmadik vektort még "szebben" írjuk:. Figyelmeztetem azonban, hogy az egyszerű kiválasztás másik példája nem biztos, hogy ezért a felelősség kizárását tapasztalt embereknek szánják. Emellett miért ne vesszük mondjuk harmadik vektornak? Végül is koordinátái kielégítik a rendszer minden egyes egyenletét és a vektorokat
, de itt némi ismeretre van szükség: három változó létezik, rendszermátrix rang - egység, ami azt jelenti alapvető döntési rendszer 3 - 1 \u003d 2 vektorból áll. A talált vektorok azonban ezen ismeretek nélkül is tökéletesen láthatók, pusztán intuitív szinten. Ebben az esetben a harmadik vektort még "szebben" írjuk:. Figyelmeztetem azonban, hogy az egyszerű kiválasztás másik példája nem biztos, hogy ezért a felelősség kizárását tapasztalt embereknek szánják. Emellett miért ne vesszük mondjuk harmadik vektornak? Végül is koordinátái kielégítik a rendszer minden egyes egyenletét és a vektorokat  lineárisan függetlenek. Ez az opció elvileg alkalmas, de "görbe", mivel a "másik" vektor az alaprendszer vektorainak lineáris kombinációja.
lineárisan függetlenek. Ez az opció elvileg alkalmas, de "görbe", mivel a "másik" vektor az alaprendszer vektorainak lineáris kombinációja.
Válasz: sajátértékek:, sajátvektorok: 
Hasonló példa önálló megoldásra:
7. példa
Keresse meg a sajátértékeket és a sajátvektorokat 
Durva példa a lecke végén végzett befejezésre.
Meg kell jegyezni, hogy mind a 6., mind a 7. példában lineárisan független sajátvektorok hármasát kapjuk, és ezért az eredeti mátrix reprezentálható a kanonikus bontásban. De ilyen málna nem minden esetben fordul elő:
8. példa

Döntés: komponálja és oldja meg a jellemző egyenletet: 
Az első oszlopnál megnyitjuk a meghatározót: 
További egyszerűsítéseket hajtunk végre a figyelembe vett módszer szerint, elkerülve a 3. fokú polinomot: 
![]() - sajátértékek.
- sajátértékek.
Keressük meg a sajátvektorokat:
1) Nincsenek nehézségek a gyökérrel: 
Ne lepődj meg, a halmaz mellett változókat is használnak - itt nincs különbség.
A 3. egyenletből kifejezzük - az 1. és a 2. egyenletben helyettesítjük: 
Mindkét egyenletből következik:
Engedje meg: 

2-3) Több érték esetén megkapjuk a rendszert  .
.
Írjuk fel a rendszer mátrixát, és elemi transzformációkkal hozzuk el lépésenként:
HOMOGÉN LINEÁRIS EGYENLETEK RENDSZERE
A homogén lineáris egyenletek rendszere a forma rendszere
Egyértelmű, hogy ebben az esetben ![]() mivel A selejtezők egyik oszlopának minden eleme nulla.
mivel A selejtezők egyik oszlopának minden eleme nulla.
Mivel az ismeretleneket a képletek találják meg ![]() , akkor abban az esetben, amikor Δ ≠ 0, a rendszernek egyedi nulla megoldása van x = y = z \u003d 0. Azonban sok problémában érdekes az a kérdés, hogy van-e egy homogén rendszernél nulla mellett más megoldás is.
, akkor abban az esetben, amikor Δ ≠ 0, a rendszernek egyedi nulla megoldása van x = y = z \u003d 0. Azonban sok problémában érdekes az a kérdés, hogy van-e egy homogén rendszernél nulla mellett más megoldás is.
Tétel. Ahhoz, hogy a lineáris homogén egyenletrendszer nem nulla megoldást kapjon, szükséges és elegendő, hogy Δ ≠ 0.
Tehát, ha a determináns Δ ≠ 0, akkor a rendszernek egyedi megoldása van. Ha Δ ≠ 0, akkor a lineáris homogén egyenletek rendszere végtelen megoldásokkal rendelkezik.
Példák.
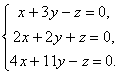
Saját vektorok és a mátrix sajátértékei
Adjunk négyzetmátrixot  , x - valamilyen mátrixoszlop, amelynek magassága egybeesik a mátrix sorrendjével A. .
, x - valamilyen mátrixoszlop, amelynek magassága egybeesik a mátrix sorrendjével A. .
Sok probléma esetén figyelembe kell venni az egyenletet a x
ahol λ valamilyen szám. Nyilvánvaló, hogy bármely λ esetén ennek az egyenletnek nulla megoldása van.
A λ számot, amelyre ennek az egyenletnek nem null megoldása van, hívjuk saját jelentése mátrixok A, és x mert ilyen λ-nak nevezzük saját vektor mátrixok A.
Keresse meg a mátrix sajátvektorát! A... Amennyiben E∙X \u003d X, akkor a mátrixegyenlet úgy írható át ![]() vagy
vagy ![]() ... Bővített formában ez az egyenlet lineáris egyenletrendszerként írható át. Igazán
... Bővített formában ez az egyenlet lineáris egyenletrendszerként írható át. Igazán  .
.
És ezért 
Tehát kaptunk egy homogén lineáris egyenletrendszert a koordináták meghatározásához x 1, x 2, x 3 vektor x... Ahhoz, hogy a rendszernek legyenek nem nulla megoldásai, szükséges és elegendő, hogy a rendszer determinánsa nulla, azaz.

Ez egy λ 3. fokú egyenlet. Ezt hívják jellegzetes egyenlet mátrixok A és a λ sajátértékek meghatározására szolgál.
Minden λ sajátérték megfelel egy sajátvektornak x, amelynek koordinátáit a rendszer határozza meg a megfelelő λ értéken.
Példák.
ALGEBRA VEKTOR. A VEKTOR FOGALMA
A fizika különféle ágainak tanulmányozása során vannak olyan mennyiségek, amelyeket teljesen meghatároznak számértékeik megadásával, például hossz, terület, tömeg, hőmérséklet stb. Az ilyen mennyiségeket skalárisnak nevezzük. Rajtuk kívül vannak azonban olyan mennyiségek is, amelyek meghatározásához a numerikus érték mellett meg kell ismerni a tér irányát is, például a testre ható erőt, a test sebességét és gyorsulását, amikor a térben mozog, a mágneses tér erősségét a tér egy adott pontjában és stb. Az ilyen mennyiségeket vektornak nevezzük.
Vezessünk be egy szigorú meghatározást.
Irányított szegmens nevezzünk egy szegmenst, amelynek végeihez viszonyítva ismert, hogy melyikük az első és melyik a második.

Vektor irányított szegmensnek nevezzük, amelynek bizonyos hosszúsága van, azaz ez egy bizonyos hosszúságú szakasz, amelyben az egyik határpontját kezdetnek, a másikat végnek vesszük. Ha egy A - a vektor kezdete, B - a végét, akkor a vektort szimbólummal jelölik, ráadásul a vektort gyakran egy betűvel jelölik. Az ábrán a vektort egy vonalszakasz, az irányát pedig egy nyíl jelöli.
Modul vagy hossz a vektor az azt meghatározó irányított szakasz hossza. || jelzi vagy ||
Az úgynevezett nulla vektor, amelynek kezdete és vége egybeesik, szintén vektorokra lesz utalva. Azt jelzik. A nulla vektornak nincs meghatározható iránya, modulusa pedig nulla || \u003d 0.
Vektorok és hívják kollinárisha ugyanazon a vonalon vagy párhuzamos vonalakon helyezkednek el. Sőt, ha a vektorok és ugyanabban az irányban vannak, akkor ellentétesen fogunk írni.
Azonos síkkal párhuzamos egyeneseken elhelyezkedő vektorokat hívjuk koplanáris.
Két vektor és hívjuk egyenlőha kollinárisak, egyformán irányítottak és hosszúak. Ebben az esetben írjon.
A vektorok egyenlőségének meghatározásából az következik, hogy egy vektor önmagával párhuzamosan átvihető, és az eredetét a tér bármely pontjára helyezheti.
például.
LINEÁRIS MŰVELETEK AZ ELEKTOROKON
- A vektor szorzása számmal.
A λ számú vektor szorzata egy új vektor, amely:
A λ számú vektor szorzatát jelöljük.

Például, egy olyan vektor, amely a vektorral azonos irányba irányul, és amelynek hossza a fele felének felel meg.
A bevezetett művelet a következő tulajdonságait:
- Vektorok összeadása.
Legyen és legyen két tetszőleges vektor. Vegyünk egy tetszőleges pontot O és szerkesszünk egy vektort. Ezek után a ponttól A tegye félre a vektort. Az első vektor kezdetét a második végével összekötő vektort hívjuk összeg ezen vektorok közül, és ezt jelöljük
 .
.
A vektorösszeadás megfogalmazott definícióját hívjuk paralelogramma szabály, mivel a vektorok azonos összege az alábbiak szerint nyerhető el. Tegye félre a ponttól O vektorok és. Építsünk egy paralelogrammát ezekre a vektorokra OABS... Mivel vektorok, akkor egy olyan vektor, amely a csúcsból húzott paralelogramma átlója O, nyilvánvalóan a vektorok összege lesz.

Könnyű ellenőrizni a következőket vektor addíciós tulajdonságok.
- A vektorok különbsége.
Egy adott vektorhoz kollináris, egyenlő hosszúságú és ellentétesen irányított vektort nevezünk szemben vektor a vektorhoz, és ezzel jelöljük. Az ellentétes vektor tekinthető annak eredményének, ha a vektort megszorozzuk a λ \u003d –1: számmal.