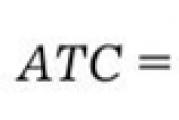A pozíció jellemzői mellett - egy valószínűségi változó átlagos, tipikus értékei - számos jellemzőt is használnak, amelyek mindegyike leírja az eloszlás egyik vagy másik tulajdonságát. Ilyen jellemzőként leggyakrabban az úgynevezett momentumokat használják.

A nyomaték fogalmát széles körben használják a mechanikában a tömegek eloszlásának leírására (statikus nyomatékok, tehetetlenségi nyomatékok stb.). Pontosan ugyanezeket a technikákat alkalmazzák a valószínűségszámításban egy valószínűségi változó eloszlásának alapvető tulajdonságainak leírására. A gyakorlatban leggyakrabban kétféle momentumot használnak: kezdeti és központi.

Egy nem folytonos valószínűségi változó s-edik sorrendjének kezdeti momentuma a következő alak összege:

. (5.7.1)

Nyilvánvaló, hogy ez a meghatározás egybeesik az s rend kezdeti momentumának mechanikai meghatározásával, ha tömegek koncentrálódnak az abszcissza tengelyen.

Egy folytonos X valószínűségi változó esetén az s-edik sorrend kezdeti momentuma az integrál

. (5.7.2)

Könnyen ellenőrizhető, hogy az előző n°-ban bevezetett pozíció fő jellemzője - a matematikai elvárás - nem más, mint a valószínűségi változó első kezdő momentuma.

A matematikai elvárás előjelét használva a két (5.7.1) és (5.7.2) képletet egyesíthetjük egybe. Valójában az (5.7.1) és (5.7.2) képletek szerkezetükben teljesen hasonlóak az (5.6.1) és (5.6.2) képletekhez, azzal a különbséggel, hogy a és helyett rendre és. Ezért írhatunk egy általános definíciót a harmadrendű kezdeti momentumra, amely mind a nem folytonos, mind a folytonos mennyiségekre érvényes:

, (5.7.3)

azok. egy valószínűségi változó harmadrendjének kezdeti momentuma ennek a valószínűségi változó harmadrendű hatványának matematikai elvárása.

A központi momentum meghatározása előtt vezessük be a „központú valószínűségi változó” új fogalmát.

Legyen egy valószínűségi változó matematikai elvárással. Egy mennyiségnek megfelelő központú valószínűségi változó egy valószínűségi változó matematikai elvárásától való eltérése:

A jövőben egyezzünk meg abban, hogy az adott valószínűségi változónak megfelelő középpontos valószínűségi változót mindenhol ugyanazzal a betűvel jelöljük, felül a jellel.

Könnyen ellenőrizhető, hogy egy központú valószínűségi változó matematikai elvárása nulla. Valóban, nem folyamatos mennyiségre

hasonlóképpen folyamatos mennyiségnél.

Egy valószínűségi változó központosítása nyilvánvalóan egyenértékű azzal, hogy az origót a középső, "központi" pontba mozgatjuk, amelynek abszcisszája megegyezik a matematikai elvárással.

A központosított valószínűségi változó pillanatait központi momentumoknak nevezzük. Hasonlóak a mechanikában a súlyponthoz viszonyított nyomatékokhoz.

Így egy valószínűségi változó s sorrendjének központi momentuma a megfelelő központú valószínűségi változó th hatványának matematikai elvárása:

, (5.7.6)

folyamatos esetén pedig az integrállal

. (5.7.8)

A továbbiakban azokban az esetekben, amikor nem kétséges, hogy az adott pillanat melyik valószínűségi változóhoz tartozik, a rövidség kedvéért az és helyett egyszerűen és írunk.

Nyilvánvaló, hogy bármely valószínűségi változó esetén az első sorrend központi momentuma egyenlő nullával:

, (5.7.9)

mivel egy központosított valószínűségi változó matematikai elvárása mindig nulla.

Vezessünk összefüggéseket a különböző rendek központi és kezdeti momentumai között. Csak a nem folytonos értékekre vonjuk le a következtetést; könnyen belátható, hogy pontosan ugyanezek az összefüggések a folytonos mennyiségekre is igazak, ha a véges összegeket integrálokkal, a valószínűségeket pedig valószínűségi elemekkel helyettesítjük.

Tekintsük a második központi pontot:

Hasonlóképpen a harmadik központi mozzanathoz ezt kapjuk:

Kifejezések stb. hasonló módon szerezhető be.

Így bármely valószínűségi változó központi momentumaira a következő képletek érvényesek:

(5.7.10)

Általánosságban elmondható, hogy a mozzanatokat nem csak az origóhoz (kezdeti pillanatok) vagy a matematikai elváráshoz (központi momentumok) viszonyítva tekinthetjük, hanem egy tetszőleges ponthoz képest is:

. (5.7.11)

A központi mozzanatoknak azonban van előnye az összes többihez képest: az első központi momentum, mint láttuk, mindig nulla, a következő, második központi momentum pedig ebben a vonatkoztatási rendszerben minimális értékű. Bizonyítsuk be. Egy helyen nem folytonos valószínűségi változó esetén az (5.7.11) képlet a következő:

. (5.7.12)

Alakítsuk át ezt a kifejezést:

Nyilvánvalóan ez az érték akkor éri el a minimumát, ha pl. amikor a pillanatot egy ponthoz viszonyítva vesszük.

A pillanatok közül az első kezdeti momentumot (matematikai várakozás) és a második központi momentumot leggyakrabban egy valószínűségi változó jellemzőiként használják.

A második központi momentumot a valószínűségi változó varianciájának nevezzük. Tekintettel többek között ennek a jellemzőnek a rendkívüli fontosságára, külön jelölést vezetünk be:

A központi momentum meghatározása szerint

, (5.7.13)

azok. egy X valószínűségi változó varianciája a megfelelő középpontos érték négyzetének matematikai elvárása.

Ha az (5.7.13) kifejezésben szereplő értéket a kifejezésére cseréljük, a következőt kapjuk:

. (5.7.14)

Az eltérés közvetlen kiszámításához használja a képleteket:

, (5.7.15)

(5.7.16)

Illetve nem folytonos és folyamatos értékekre.

A valószínűségi változó diszperziója a diszperzió jellemzője, egy valószínűségi változó értékeinek diszperziója a matematikai elvárása körül. Maga a „diszperzió” szó „diszperziót” jelent.

Ha rátérünk az eloszlás mechanikus értelmezésére, akkor a diszperzió nem más, mint egy adott tömegeloszlás tehetetlenségi nyomatéka a súlyponthoz viszonyítva (matematikai elvárás).

Egy valószínűségi változó varianciája a valószínűségi változó négyzetének dimenziójával rendelkezik; a szórás vizuális jellemzőjére célszerűbb olyan mennyiséget használni, amelynek mérete egybeesik egy valószínűségi változó dimenziójával. Ehhez a variancia négyzetgyökét kivonjuk. A kapott értéket a valószínűségi változó szórásának (egyébként "standard") nevezik. A szórást a következőkkel jelöljük:

, (5.7.17)

A jelölés egyszerűsítése érdekében gyakran használjuk a szórás és a variancia rövidítéseit: és. Abban az esetben, ha nem kétséges, hogy ezek a jellemzők melyik valószínűségi változóra vonatkoznak, néha elhagyjuk az x y és és jelet egyszerűen és írjuk. A "szórás" szavakat néha lerövidítik az effektív betűk helyettesítésére.

A gyakorlatban gyakran használnak olyan képletet, amely egy valószínűségi változó varianciáját fejezi ki a második kezdeti momentum (a képlet (5.7.10.) második) alapján. Az új jelölésben ez így fog kinézni:

A matematikai elvárás és a variancia (vagy az átlagos másodfokú eltérés) a valószínűségi változók leggyakrabban használt jellemzői. Jellemezik az eloszlás legfontosabb jellemzőit: helyzetét és a szóródás mértékét. Az eloszlás részletesebb leírásához magasabb rendű momentumokat használunk.

A harmadik központi pont az eloszlás aszimmetriájának (vagy "ferdítésének") jellemzésére szolgál. Ha az eloszlás szimmetrikus a matematikai elváráshoz képest (vagy mechanikus értelmezésben a tömeg szimmetrikusan oszlik el a súlypont körül), akkor minden páratlan sorrendű momentum (ha létezik) nullával egyenlő. Sőt, összesen

ha az eloszlás szimmetrikus az eloszlási törvényhez képest és páratlan, akkor minden pozitív tag egy vele abszolút értékben egyenlő negatív tagnak felel meg, így a teljes összeg nulla. Ugyanez nyilvánvalóan igaz az integrálra is

,

amely egyenlő nullával, mint integrál egy páratlan függvény szimmetriatartományában.

Ezért természetes, hogy az eloszlási aszimmetria jellemzőjeként a páratlan momentumok valamelyikét választjuk. Ezek közül a legegyszerűbb a harmadik központi pont. Egy valószínűségi változó kockájának mérete van: dimenzió nélküli karakterisztikához a harmadik momentumot elosztjuk a szórás kockájával. A kapott értéket "aszimmetria-együtthatónak" vagy egyszerűen "aszimmetriának" nevezik; kijelöljük:

ábrán. Az 5.7.1 két ferde eloszlást mutat; az egyik (I. görbe) pozitív aszimmetriával rendelkezik (); a másik (II. görbe) negatív ().

A negyedik központi momentum az úgynevezett „hűvösség” jellemzésére szolgál, azaz. csúcsos vagy lapos tetejű eloszlás. Ezeket az eloszlási tulajdonságokat az úgynevezett kurtosis segítségével írjuk le. Egy valószínűségi változó többlete a mennyiség

A 3-as számot levonjuk az arányból, mert egy nagyon fontos és a természetben elterjedt normális eloszlási törvényhez (melyet később fogunk részletesen megismerni). Így normál eloszlás esetén a kurtosis nulla; a normálnál csúcsosabb görbéknek pozitív a görbülete; több lapos tetejű görbület - negatív kurtosis.

ábrán. Az 5.7.2 bemutatja: normál eloszlás (I. görbe), eloszlás pozitív görbével (II. görbe) és eloszlás negatív görbével (III. görbe).

A fent vizsgált kezdeti és központi momentumok mellett a gyakorlatban néha az úgynevezett abszolút momentumokat (kezdeti és központi) alkalmazzák, amelyeket a képletek határoznak meg.

Nyilvánvalóan a páros rendelések abszolút mozzanatai egybeesnek a megszokott pillanatokkal.

Az abszolút momentumok közül a leggyakrabban az első abszolút középső momentumot használják.

, (5.7.21)

számtani középnek nevezzük. A szórással és a szórással együtt a számtani átlagot is gyakran használják a diszperzió jellemzőjeként.

A valószínűségi változók leggyakrabban használt numerikus jellemzői a matematikai várakozás, módusz, medián, kezdeti és centrális momentumok, és különösen a variancia, a szórás, a ferdeség és a görbület. Sok gyakorlati feladatban a valószínűségi változó teljes karakterisztikája - az eloszlási törvény - vagy nem szükséges, vagy nem szerezhető be. Ezekben az esetekben a valószínűségi változó hozzávetőleges leírására korlátozódnak segítséggel. Numerikus jellemzők, amelyek mindegyike az eloszlás valamilyen jellemző tulajdonságát fejezi ki.

Nagyon gyakran numerikus jellemzőket használnak arra, hogy megközelítőleg helyettesítsék az egyik eloszlást egy másikkal, és általában arra törekednek, hogy ezt a cserét úgy hajtsák végre, hogy több fontos pont változatlan maradjon.

Példa 1. Elvégzünk egy kísérletet, aminek eredményeként előfordulhat, hogy nem jelenik meg egy esemény, amelynek valószínűsége egyenlő. Valószínűségi változót veszünk figyelembe - egy esemény előfordulásának számát (egy esemény jellemző valószínűségi változóját). Határozza meg jellemzőit: matematikai elvárás, szórás, szórás.

Megoldás. A mennyiség eloszlási sorozatának alakja:

hol van annak a valószínűsége, hogy az esemény nem jelenik meg.

Az (5.6.1) képlet segítségével megtaláljuk az érték matematikai elvárását:

A mennyiség szórását az (5.7.15) képlet határozza meg:

(Azt javasoljuk, hogy az olvasó ugyanazt az eredményt kapja, ha a varianciát a második kezdeti momentumban fejezi ki).

2. példa Három független lövést adnak le a célpontra; az egyes lövések eltalálásának valószínűsége 0,4. véletlen változó - a találatok száma. Határozza meg egy mennyiség jellemzőit - matematikai elvárás, szórás, effektív, aszimmetria.

Megoldás. A mennyiség eloszlási sorozatának alakja:

Kiszámoljuk a mennyiség numerikus jellemzőit:

Megjegyezzük, hogy ugyanazok a jellemzők sokkal könnyebben kiszámíthatók a függvények numerikus jellemzőire vonatkozó tételek használatával (lásd a 10. fejezetet).

Ez a jellemző azonban önmagában még mindig nem elegendő egy valószínűségi változó tanulmányozásához. Képzelj el két lövöldözőt, akik célba lőnek. Az egyik pontosan lő és közel üt a középponthoz, a másik pedig... csak szórakozik és nem is céloz. De ami vicces, az az övé átlagos az eredmény pontosan ugyanaz lesz, mint az első lövésznél! Ezt a helyzetet hagyományosan a következő valószínűségi változók illusztrálják:

A "mesterlövész" matematikai elvárás viszont egy "érdekes személyiségnél" egyenlő: - az is nulla!

Ezért számszerűsíteni kell, hogy meddig elszórt golyók (egy valószínűségi változó értékei) a cél középpontjához képest (matematikai elvárás). jól és szétszóródás latinból csak úgy fordítják diszperzió .

Nézzük meg, hogyan határozható meg ez a numerikus jellemző a lecke 1. részének egyik példájában:

Ott találtunk egy csalódást keltő matematikai elvárást a játékkal kapcsolatban, és most ki kell számítanunk a szórását, ami jelöljükát .

Nézzük meg, hogy a győzelmek/veszteségek mennyire „szóródtak” az átlaghoz képest. Nyilván ehhez számolni kell különbségek között egy valószínűségi változó értékeiés ő matematikai elvárás:

–5 – (–0,5) = –4,5
2,5 – (–0,5) = 3
10 – (–0,5) = 10,5

Most úgy tűnik, össze kell foglalni az eredményeket, de ez az út nem megfelelő - azért, mert a bal oldali ingadozások a jobb oldali ingadozásokkal kiegyenlítődnek. Tehát például egy "amatőr" lövész (példa fent) a különbség az , és hozzáadva nullát ad, így nem kapunk becslést a kilövésének szórására.

Ha meg akarja kerülni ezt a kellemetlenséget, fontolja meg modulok különbségek, de technikai okokból a megközelítés gyökeret vert, amikor négyzetre emelik. Kényelmesebb a megoldást táblázattal elkészíteni:

És itt számolni kell súlyozott átlag az eltérések négyzeteinek értéke. Mi az? Az övék várható érték, ami a szórás mértéke:

– meghatározás variancia. A definícióból azonnal kiderül, hogy szórás nem lehet negatív- gyakorlathoz vedd figyelembe!

Emlékezzünk arra, hogyan találjuk meg az elvárást. A különbségek négyzetét megszorozzuk a megfelelő valószínűségekkel (A táblázat folytatása):
- átvitt értelemben ez "húzóerő",
és foglalja össze az eredményeket:

Nem gondolja, hogy a nyeremények hátterében túl nagynak bizonyult az eredmény? Így van – négyzeteztünk, és ahhoz, hogy visszatérjünk játékunk dimenziójához, ki kell vonnunk a négyzetgyököt. Ezt a mennyiséget ún szórás és a görög "szigma" betűvel jelöljük:

Ezt az értéket néha hívják szórás .

mi a jelentése? Ha a matematikai elvárástól balra és jobbra a szórással térünk el:

- akkor a valószínűségi változó legvalószínűbb értékei "koncentrálódnak" erre az intervallumra. Amit valójában megfigyelünk:

Történt azonban, hogy a szóródás elemzésekor szinte mindig a szóródás fogalmával operálunk. Lássuk, mit jelent ez a játékokkal kapcsolatban. Ha a nyilak esetében a találatok "pontosságáról" beszélünk a célpont középpontjához képest, akkor itt a szórás két dolgot jellemez:

Először is nyilvánvaló, hogy az arányok növekedésével a szórás is nő. Tehát például, ha 10-szeresére növeljük, akkor a matematikai elvárás tízszeresére, a szórás pedig 100-szorosára nő. (amíg ez másodfokú mennyiség)... De vegye figyelembe, hogy a játékszabályok nem változtak! Csak az árfolyamok változtak, nagyjából 10 rubelt fogadtunk, most 100.

A második, érdekesebb pont az, hogy a játékstílust a szóródás jellemzi. Mentálisan rögzítsük a játékarányokat egy bizonyos szinten, és nézd meg, mi van itt:

Az alacsony varianciájú játék óvatos játék. A játékos hajlamos a legmegbízhatóbb sémák kiválasztására, és bizonytalan helyzetben nem fogad túl sok pénzt. Például a piros/fekete rendszer a rulettben (lásd a cikk 4. példáját Véletlen változók) .

Magas varianciájú játék. Gyakran hívják szétszórt játszma, meccs. Ez egy kalandos vagy agresszív játékstílus, ahol a játékos adrenalint pumpáló sémákat választ. Emlékezzünk legalább Martingale, amelyben az előző bekezdés "csendes" játékánál nagyságrendekkel nagyobb összegek forognak kockán.

A póker helyzete jelzésértékű: vannak ún szoros olyan játékosok, akik hajlamosak óvatosak lenni és "mozogni" játékeszközeiken (bankroll alapján)... Nem meglepő módon a bankrolljuk nem ingadozik sokat (alacsony szórás). Ellenkezőleg, ha egy játékosnak nagy a szórása, akkor ez az agresszor. Gyakran kockáztat, nagy téteket köt, és egyszerre tud hatalmas bankot feltörni, és összetörni.

Ugyanez történik a Forexben, más tőzsdékben és így tovább – sok példa van rá.

Sőt, minden esetben nem mindegy – hogy a játék egy fillérről vagy több ezer dollárról szól. Minden szintnek megvannak a maga alacsony és nagy szórású játékosai. Nos, az átlagos fizetésért, mint emlékszünk, "felelős" várható érték.

Valószínűleg észrevette, hogy a szórás megtalálása hosszú és fáradságos folyamat. De a matematika nagyvonalú:

A variancia megállapításának képlete

Ez a képlet közvetlenül a variancia definíciójából származik, és azonnal forgalomba hozzuk. A tányér tetejét másolom a játékunkkal:

és a megtalált elvárás.

Számítsuk ki a szórást a második módon. Először is megtaláljuk a matematikai elvárást - egy valószínűségi változó négyzetét. Által az elvárás meghatározása:

Ebben az esetben:

Tehát a képlet szerint:

Érezd a különbséget, ahogy mondják. A gyakorlatban pedig természetesen jobb a képlet alkalmazása (hacsak a feltétel másként nem kívánja).

Elsajátítjuk a megoldás és a tervezés technikáját:

6. példa

Keresse meg annak matematikai elvárását, szórását és szórását.

Ez a feladat mindenhol megtalálható, és általában értelmetlen.
Elképzelhetsz több számmal ellátott izzót, amelyek bizonyos valószínűséggel kigyulladnak egy őrültek házában :)

Megoldás: Az alapvető számításokat kényelmesen összefoglaljuk egy táblázatban. Először az eredeti adatokat írjuk a felső két sorba. Ezután kiszámoljuk a termékeket, majd végül az összegeket a jobb oldali oszlopban:

Valójában szinte minden készen áll. A harmadik sor egy kész matematikai elvárást tartalmaz: .

Az eltérést a következő képlettel számítjuk ki:

És végül a szórás:
- én személy szerint 2 tizedesjegyig szoktam kerekíteni.

Minden számítás elvégezhető számológépen, vagy még jobb - Excelben:

itt nehéz hibázni :)

Válasz:

Azok, akik szeretnék, tovább egyszerűsíthetik életüket, és használhatják az én számológép (demó), amely nem csak azonnal megoldja ezt a problémát, hanem épít is tematikus diagramok (hamarosan odaérünk)... A program képes letöltés a könyvtárban- ha legalább egy oktatási anyagot feltöltött, vagy beszerez Egy másik módja... Köszönjük a projekt támogatását!

Néhány feladat az önálló megoldáshoz:

7. példa

Számítsa ki egy valószínűségi változó szórását az előző példából definíció alapján!

És egy hasonló példa:

8. példa

Egy diszkrét valószínűségi változót saját eloszlási törvénye határoz meg:

Igen, egy valószínűségi változó értékei elég nagyok lehetnek (példa valódi munkából), és itt, ha lehetséges, használja az Excelt. Ahogy egyébként a 7. példában - gyorsabb, megbízhatóbb és élvezetesebb.

Megoldások és válaszok az oldal alján.

A lecke 2. részének zárásaként még egy tipikus problémát elemezünk, mondhatnánk egy kis rebuszt is:

9. példa

Egy diszkrét valószínűségi változó csak két értéket vehet fel: és ráadásul. A valószínűség, a matematikai elvárás és a szórás ismert.

Megoldás: Kezdjük egy ismeretlen valószínűséggel. Mivel egy valószínűségi változó csak két értéket vehet fel, a megfelelő események valószínűségeinek összege:

és azóta is.

Már csak meg kell találni... könnyű ezt mondani :) De hát menjünk. A matematikai elvárás definíciója szerint:
- behelyettesítjük az ismert értékeket:

- és ebből az egyenletből semmi mást nem lehet kipréselni, csak azt, hogy átírhatod a szokásos irányba:

vagy:

Azt hiszem, sejtheti a további lépéseket. Állítsuk össze és oldjuk meg a rendszert:

A tizedes törtek természetesen teljes szégyen; szorozd meg mindkét egyenletet 10-zel:

és oszd el 2-vel:

Ez jobb. Az 1. egyenletből a következőket fejezzük ki:
(ez egy egyszerűbb módszer)- behelyettesítjük a 2. egyenletbe:

felállítunk négyzet alakúés egyszerűsítsünk:

Szorozva:

Az eredmény az másodfokú egyenlet, megtaláljuk a diszkriminálóját:
- tökéletes!

és két megoldást kapunk:

1) ha , azután ;

2) ha , azután .

Az első értékpár megfelel a feltételnek. Nagy valószínűséggel minden helyes, de ennek ellenére írjuk az elosztási törvényt:

és ellenőrizzük, hogy megtaláljuk az elvárást:

Diszperzió Egy valószínűségi változó (szórása) a valószínűségi változó matematikai elvárásától való eltérésének négyzetének matematikai elvárása:

A szórás kiszámításához használhatja a kissé átalakított képletet

mivel M (X), 2 és
- állandó értékek. Ily módon

4.2.2. Diszperziós tulajdonságok

1. tulajdonság. Az állandó szórása nulla. Valóban, definíció szerint

2. tulajdonság. A konstans tényező kivehető a varianciajelből, és négyzetre emelhető.

Bizonyíték

Középre állított a valószínűségi változó egy valószínűségi változónak a matematikai elvárásától való eltérése:

A központosított mennyiségnek két olyan tulajdonsága van, amelyek kényelmesek az átalakításhoz:

3. tulajdonság. Ha a valószínűségi változók X és Y akkor független

Bizonyíték... jelöljük
... Azután.

A második tagban a valószínűségi változók függetlensége és a központosított valószínűségi változók tulajdonságai miatt

4.5. példa. Ha aés bÁllandók, akkor D (aX +b)= D(aX) +D(b)=
.

4.2.3. Szórás

A diszperziónak, mint egy valószínűségi változó terjedésének jellemzője, van egy hátránya. Ha pl. x- a mérési hibának méretei vannak MM, akkor a szórásnak van dimenziója
... Ezért gyakran szívesebben használják a terjedés egy másik jellemzőjét - szórás , ami egyenlő a variancia négyzetgyökével

A szórás mérete ugyanaz, mint magának a valószínűségi változónak.

4.6. példa. Egy esemény előfordulási számának szórása a független tesztsémában

Gyártva n független tesztek és egy esemény bekövetkezésének valószínűsége minden tesztben egyenlő R... Adjuk meg, mint korábban, az esemény előfordulásának számát x az egyes kísérletekben előforduló események számán keresztül:

Mivel a kísérletek függetlenek, ezért a kísérletekhez társított valószínűségi változók független. És a függetlenség miatt nekünk van

De mindegyik valószínűségi változónak van eloszlási törvénye (3.2. példa)

és
(4.4. példa). Ezért a variancia meghatározása szerint:

ahol q=1- p.

Ennek eredményeként megvan
,

Egy esemény előfordulási számának szórása in n független kísérletek egyenlő
.

4.3. Valószínűségi változók pillanatai

A már figyelembe vetteken kívül a valószínűségi változók számos más numerikus jellemzővel is rendelkeznek.

A kiindulópont k x (
) matematikai elvárásnak nevezzük k ennek a valószínűségi változónak a hatványa.

Központi pont k egy valószínűségi változó harmadrendje x matematikai elvárásnak nevezzük k a megfelelő középpontos érték hatványa.

Könnyen belátható, hogy az elsőrendű központi momentum mindig nulla, a másodrendű központi momentum egyenlő a szórással, hiszen.

A harmadik rend központi momentuma képet ad egy valószínűségi változó eloszlásának aszimmetriájáról. A másodiknál ​​magasabb rendű mozzanatokat viszonylag ritkán használjuk, ezért csak a fogalmakra szorítkozunk.

4.4. Példák az elosztási törvények megtalálására

Nézzünk példákat a valószínűségi változók eloszlási törvényeinek és numerikus jellemzőinek megtalálására.

4.7. példa.

Rajzolja fel a célt érő találatok számának eloszlási törvényét három célba lövés esetén, ha az egyes lövésekkel való eltalálás valószínűsége 0,4! Keresse meg az integrálfüggvényt F(X) egy diszkrét valószínűségi változó kapott eloszlására xés rajzold le a menetrendjét. Keresse meg a várható értéket M(x) , szórás D(x) és szórása
(x) egy valószínűségi változó x.

Megoldás

1) Diszkrét valószínűségi változó x- három lövéssel a célt ért találatok száma - négy értéket vehet fel: 0, 1, 2, 3 ... Annak valószínűségét, hogy mindegyiket elfogadja, a Bernoulli-képlet alapján találjuk meg: n=3,p=0,4,q=1- p= 0,6 és m=0, 1, 2, 3:

Megkapjuk a lehetséges értékek valószínűségét x:;

Állítsuk össze egy valószínűségi változó szükséges eloszlási törvényét x:

Kontroll: 0,216 + 0,432 + 0,288 + 0,064 = 1.

Szerkesszük meg a kapott valószínűségi változó eloszlási sokszögét x... Ehhez téglalap alakú koordinátarendszerben jelölje be a pontokat (0; 0,216), (1; 0,432), (2; 0,288), (3; 0,064). Ezeket a pontokat vonalszakaszokkal kötjük össze, a kapott vonallánc a kívánt eloszlási sokszög (4.1. ábra).

2) Ha x 0, akkor F(X)= 0. Valójában a nullánál kisebb értékek a mennyiség x nem fogadja el. Ezért mindenkinek x0 a definíció használatával F(X), kapunk F(X)=P(x< x) = 0 (mint egy lehetetlen esemény valószínűsége).

Ha 0 , azután F(x) = 0,216. Valóban, ebben az esetben F(X)=P(x< x) = =P(- < x 0)+ P(0< x< x) =0,216+0=0,216.

Ha vesszük pl. x= 0,2, akkor F(0,2)=P(x<0,2) ... De az esemény valószínűsége x<0,2 равна 0,216, так как случайная величинаx csak egy esetben vesz fel 0,2-nél kisebb értéket, mégpedig 0 0,216 valószínűséggel.

Ha 1 , azután

Igazán, x felveheti a 0 értéket 0,216 valószínűséggel, az 1 értéket pedig 0,432 valószínűséggel; ezért e jelentések egyike, bármi legyen is az, x el tudja fogadni (az inkonzisztens események valószínűségeinek összeadási tételével) 0,648 valószínűséggel.

Ha 2 , majd hasonló módon érvelve megkapjuk F(X)= 0,216 + 0,432 + + 0,288 = 0,936. Valóban, hagyjuk, hogy pl. x= 3. Azután F(3)=P(x<3) egy esemény valószínűségét fejezi ki x<3 – стрелок сделает меньше трех попаданий, т.е. ноль, один или два. Применяя теорему сложения вероятностей, получим указанное значение функцииF(X).

Ha x> 3, akkor F(X)= 0,216 + 0,432 + 0,288 + 0,064 = 1. Valóban, az esemény x
megbízható és valószínűsége egyenlő eggyel, és x> 3 – lehetetlen. Tekintve, hogy

F(X)=P(x< x) =P(x 3) + P(3< x< x) , a megadott eredményt kapjuk.

Így megkapjuk az X valószínűségi változó szükséges integráleloszlási függvényét:

F(x) =

melynek grafikonja az ábrán látható. 4.2.

3) Egy diszkrét valószínűségi változó matematikai elvárása egyenlő az összes lehetséges érték szorzatának összegével x a valószínűségükről:

M (X)=0=1,2.

Azaz átlagosan három lövéssel egy találatot ér a cél.

A variancia a variancia definíciója alapján számítható ki D(x)= M(x- M(x)) vagy használja a képletet D(x)= M(x
, ami gyorsabban vezet a célhoz.

Írjuk fel egy valószínűségi változó eloszlásának törvényét x :

Keresse meg a matematikai elvárást x:

M (X ) = 04
= 2,16.

Számítsuk ki a szükséges szórást:

D(x) = M(x ) – (M(x)) = 2,16 – (1,2)= 0,72.

A szórást a képlet alapján találjuk meg

(x) =
= 0,848.

intervallum ( M- ; M+ ) = (1,2-0,85; 1,2 + 0,85) = (0,35; 2,05) - a valószínűségi változó legvalószínűbb értékeinek intervalluma x, 1 és 2 érték esik bele.

4.8. példa.

Adott egy folytonos valószínűségi változó differenciális eloszlásfüggvénye (sűrűségfüggvénye). x:

f(x) =

1) Határozza meg az állandó paramétert! a.

2) Keresse meg az integrálfüggvényt! F(x) .

3) Készítsen függvénygrafikonokat f(x) és F(x) .

4) Keresse meg a valószínűségeket kétféleképpen P (0,5< x 1,5) és P(1,5< x<3,5) .

5). Keresse meg a várható értéket M (X), szórás D(X)és szórása
valószínűségi változó x.

Megoldás

1) Differenciálfüggvény tulajdonság szerint f(x) ki kell elégítenie a feltételt
.

Számítsuk ki ezt a nem megfelelő integrált az adott függvényre f(x) :

Ezt az eredményt behelyettesítve az egyenlőség bal oldalába, azt kapjuk a= 1. A megfelelő állapotban f(x) cserélje ki a paramétert a 1-től:

2) Megtalálni F(x) képletet fogjuk használni

.

Ha x
, azután
, ennélfogva,

Ha 1
azután

Ha x> 2, akkor

Tehát a szükséges integrálfüggvény F(x) úgy néz ki, mint a:

3) Készítsünk függvénygráfokat f(x) és F(x) (4.3. és 4.4. ábra).

4) Egy valószínűségi változó eltalálásának valószínűsége egy adott intervallumban (a,b) képlettel számítjuk ki
ha a függvény ismert f(x), és a képlet szerint P(a < x < b) = F(b) – F(a), ha a függvény ismert F(x).

megtalálja
két képlet segítségével, és hasonlítsa össze az eredményeket. Feltétel szerint a = 0,5;b=1,5; funkció f(x) pontban meghatározott). Ezért a képlet által kívánt valószínűség egyenlő:

Ugyanez a valószínűség számítható ki a b) képlettel a 2) pontban kapott növekményen keresztül. integrál funkció F(x) ezen az intervallumon:

Mivel F(0,5)=0.

Hasonlóképpen találjuk

mivel F(3,5)=1.

5) Megtalálni a matematikai elvárást M (X) képletet fogjuk használni
Funkció f(x) pont megoldásában megadott), az (1,2] intervallumon kívül nullával egyenlő:

Folytonos valószínűségi változó diszperziója D(X) az egyenlőség határozza meg

, vagy ennek megfelelő egyenlőség

.

Mert lelet D(x) az utolsó képletet használjuk, és figyelembe vesszük az összes lehetséges értéket f(x) az (1,2] intervallumhoz tartoznak:

Szórás
=
=0,276.

Egy valószínűségi változó legvalószínűbb értékeinek intervalluma x egyenlő

(M-
, M+
) = (1,58-0,28; 1,58+0,28) = (1,3; 1,86).

Gyakorlati feladatok megoldása során olyan valószínűségi változókkal találkozhatunk, amelyek eltérő eloszlásúak, de ugyanazok a matematikai elvárások. Ezen túlmenően ezen értékek némelyike ​​kis mértékben eltér a matematikai elvárásoktól, míg mások éppen ellenkezőleg, jelentősek lehetnek. Más szóval, az értékek eltérő értékszórással rendelkezhetnek a matematikai elvárás körül.

Például két diszkrét valószínűségi változóra, amelyet a következő törvények határoznak meg:

x	-1			és	Y	-100
R	0,3	0,4	0,3	R	0,2	0,6	0,2

a matematikai elvárások egyenlőek, i.e. M(x)=M(Y) = 0. Nyilvánvaló azonban, hogy ezek különböző valószínűségi változók, és mindenekelőtt az értékek szóródása az abszcissza mentén a 0 ponttól balra és jobbra - a matematikai várakozásuk.

A fenti érvelés azt sugallja, hogy célszerű lenne figyelembe venni néhány, a szórással kapcsolatos numerikus jellemzőt. Első pillantásra úgy tűnhet, hogy egy ilyen jellemző lehet egy valószínűségi változó lehetséges értékeinek összes eltérésének átlagértéke a matematikai elvárásoktól.

Egy valószínűségi változó eltérése x a matematikai elvárásodból M(x) a valószínűségi változó és a matematikai elvárása közötti különbséget ún.

Nyilvánvalóan az eltérés is véletlenszerű érték. Határozzuk meg az eltérés átlagos értékét, i.e. az eltérés matematikai elvárását kapjuk M(x – M(x)) = M(x) – M(M(x)) =M(x) – M(x) = 0.

Tehát egy valószínűségi változó eltérésének matematikai elvárása nullával egyenlő. Ez a tény azzal is magyarázható, hogy a lehetséges eltérésértékek pozitív és negatív előjelűek is, ezért az átlagérték (matematikai várakozás) megtalálásakor a feltételek kölcsönösen törlődnek. Ez elkerülhető az eltérési értékek negatív előjeleinek eltávolításával. Ehhez ezeket az értékeket abszolút értékben vagy négyzetben veszik. Az első módot rendkívül ritkán használják, mivel az abszolút értékekkel való munka általában komoly nehézségeket okoz, például a megkülönböztetésben. Ezért az eltérés négyzetének matematikai elvárását használjuk a szórás jellemzőjeként.

Diszperzió D(x) valószínűségi változó x egy adott valószínűségi változó matematikai elvárásától való eltérésének négyzetének matematikai elvárása, azaz.

D(x) = M[(x – M(x)) 2 ] (6.4)

Maga a „diszperzió” szó „diszperziót” jelent.

Könnyű megérteni, hogy a valószínűségi változók értékeinek valószínűsége xés ( x – M(x)) 2 ugyanaz. Annak érdekében, hogy az érték ( x – M(x)) 2 felvette például az értéket, ( x 1 – M(x)) 2, elegendő, ha a valószínűségi változó x felvette a jelentését x egy . Ennek az eseménynek a valószínűsége R 1 tehát annak a valószínűsége, hogy a mennyiség ( x – M(x)) 2 veszi fel az értéket ( x 1 – M(x)) 2 is egyenlő R egy . Hasonló a helyzet a többi lehetséges értékkel is. Ezért a (6.4) képlet, figyelembe véve egy valószínűségi változó matematikai elvárásának meghatározását, a következő alakot ölti majd:

véges értékhalmazú diszkrét valószínűségi változóhoz

folytonos valószínűségi változóhoz

(6.6)

A (6.6) képletben lévő nem megfelelő integrál egy véges intervallumon át határozott integrállá változik, ha egy folytonos valószínűségi változó értékei csak ebben az intervallumban állnak rendelkezésre.

A matematikai elvárásnak ugyanaz a dimenziója, mint magának a valószínűségi változónak, ellentétben a varianciával, amelynek dimenziója megegyezik a valószínűségi változó dimenziójának négyzetével. Így a variancia nem magát a szórást, hanem egy valószínűségi változó értékeinek négyzetes szórását jellemzi. Magának az átlagos szórásnak a meghatározásához meg kell találni a variancia négyzetgyökét, és egy új numerikus karakterisztikát kapunk, amelyet szórásnak nevezünk.

Szórás σ (x) egy valószínűségi változó x a variancia négyzetgyökének nevezzük, azaz.

.

Példa 6.6 ... Határozzuk meg egy diszkrét valószínűségi változó varianciáját, amelyet a következő eloszlási sorozat adja!

Számítások után megkapjuk

(x- M(x)) 2	1,69	0,09	7,29
R	0,3	0,5	0,2

Határozzuk meg a kapott valószínűségi változó matematikai elvárását: D(x) = M[(x – M(x)) 2] = 1,69 · 0,3 + 0,09 · 0,5 + 7,29 · 0,2 = 2,01. ■

Példa 6.7 ... Határozzuk meg egy folytonos valószínűségi változó sűrűségfüggvényével adott varianciáját: f(x)=0,5x nál nél xÎ (0,2); másoknak x a sűrűségfüggvény nulla.

Megoldás ... A (6.2) képlet segítségével megtaláljuk a matematikai elvárást, megkapjuk

A (6.6) képlet segítségével megtaláljuk a szórást, és a nem megfelelő integrál egy adott intervallumon (0.2) egy bizonyosra változik:

. ■

A variancia kiszámításához gyakran más képletet is használnak, amely könnyen beszerezhető a (6.4) képletből.

6.1. Tétel. Egy valószínűségi változó varianciája egyenlő a valószínűségi változó négyzetének matematikai elvárása és a matematikai elvárás négyzete közötti különbséggel:

D(x) = M(x 2) – M 2 (x) (6.7)

Bizonyíték.Átalakítjuk a (6.4) képletet, felhasználva a matematikai elvárás tulajdonságait, megkapjuk

A tétel bizonyítva van.

Példa 6.8 ... Oldjuk meg a 6.6. példát a (6.7) képlet segítségével. A matematikai elvárást megtaláltuk, egyenlő M(x) = 2,3. Most megtaláljuk a mennyiség eloszlási törvényét x 2, megkapjuk

x 2
R	0,3	0,5	0,2

megtalálja M(x 2) = 1 0,3 + 4 0,5 + 25 0,2 = 7,3. Akkor a szórás az

D(x) = 7,3 – (2,3) 2 = 2,01. ■

Nyilvánvaló, hogy a (6.7) képlet alkalmazása nagyban leegyszerűsíti a variancia megtalálásának folyamatát. Nyilvánvaló, hogy ugyanez a képlet használható egy folytonos valószínűségi változó varianciájának meghatározására.

Diszperziós tulajdonságok

Egy valószínűségi változó varianciája a következő tulajdonságok:

1. Egy állandó érték varianciája egyenlő nullával; D(C) = 0, ahol VAL VEL- állandó érték.

Bizonyíték. A variancia meghatározásával a matematikai elvárás tulajdonságának felhasználásával azt kapjuk

D(VAL VEL) = M[(VAL VEL – M(VAL VEL)) 2 ]= M[(VAL VEL – VAL VEL) 2 ] =M(0)= 0.

Ez az eredmény teljesen nyilvánvaló, mivel a konstans csak egy értéket vesz fel, így nincs szóródás az értékekben.

Az ingatlan bizonyított.

2. A diszperziós előjelből négyzetre emelve ki lehet venni egy állandó tényezőt, azaz. D(CX) = VAL VEL 2 D(x).

Bizonyíték... A variancia meghatározásával a matematikai elvárás tulajdonságainak felhasználásával azt kapjuk

D(SH) = M[(SH – M(SH)) 2 ]=M[(SH – CM(x)) 2 ]=M[VAL VEL 2 (x – M(x)) 2 ]=

= C 2 M[(x – M(x)) 2 ]=VAL VEL 2 D(x).

Az ingatlan bizonyított.

3. Két független valószínűségi változó összegének szórása egyenlő ezen értékek szórásának összegével, vagyis ha az értékek xés Y akkor független

D(X + Y) = D(x) + D(Y).

Bizonyíték... A bizonyításhoz a (6.7) képletet alkalmazzuk és a matematikai elvárás tulajdonságait kapjuk

D(X + Y) = M((X + Y) 2) – M 2 (X + Y)=M(x 2 +2XY + Y 2) – (M(X + Y)) 2 =

=M(x 2) + M(2XY) + M(Y 2) – (M(x)+M(Y)) 2 = M(x 2) + 2M(x)M(Y) + M(Y 2) – – M 2 (x) –2M(x)M(Y) - M 2 (Y) = M(x 2) – M 2 (x) + M(Y 2) –M 2 (Y) = D(x) + D(Y).

Az ingatlan bizonyított.

Következmény. Több független mennyiség összegének szórása egyenlő ezen mennyiségek szórásának összegével.

A bizonyítást matematikai indukciós módszerrel lehet elvégezni.

4. Két független valószínűségi változó különbségének szórása egyenlő szórásaik összegével, azaz D(x–Y) = D(x) + D(Y).

Bizonyíték... A variancia második és harmadik tulajdonságát alkalmazva megkapjuk D(x–Y) = D(x) + D(– Y) = D(x) + (–1) 2 D(Y) = D(x) + D(Y).

Az ingatlan bizonyított.

A bizonyított tulajdonság könnyen kiterjeszthető tetszőleges számú független valószínűségi változóra.

Példa 6.9 ... Határozzuk meg egy diszkrét valószínűségi változó varianciáját x egyenlő az esemény előfordulásának számával A v n független tesztek, ha az előfordulás valószínűsége A minden tesztben állandó és egyenlő R.

Megoldás. Legyen a valószínűségi változó x- az esemény előfordulásának száma A v n tesztek.

Vezessük be azt is n Véletlen változók:

x 1 - az esemény előfordulásának száma A az első tárgyaláson;

x 2 - az esemény előfordulásának száma A a második tárgyalásban;

…………………………………………………………….

X n- az esemény előfordulásának száma A v n- a teszt.

Ez nyilvánvaló x=x 1 +x 2 +…+X n... A mennyiségek x 1 , x 2 , …, x n egymástól függetlenek, mivel az egyes kísérletek kimenetele nem függ a többi eredményétől. A variancia negyedik tulajdonságának következményét felhasználva megkapjuk

D(x) = D(x 1) + D(x 2) + …+ D(x n).

Határozzuk meg a mennyiség szórását x egy . Ennek a mennyiségnek az eloszlási sorozata a következő:

x 1
R	1−R	R

Azután M(x 1) = R; M(x 1 2) = R; D(x 1) = R – R 2 = R(1 – p)=pq.

Nyilvánvalóan a többi valószínűségi változó varianciája is egyenlő pq... Így

D(x) = D(x 1)+D(x 2)+…+D(x n) = npq. ■

Ha olyan valószínűségi változót vizsgálunk, amelynek értékei kellően nagy számok, akkor ettől az értéktől át lehet lépni az egyszerűbb értékekre, amelyeket középre állítottnak és standardnak nevezünk.

Meghatározás.Diszperzió (diszperzió) diszkrét valószínűségi változó a valószínűségi változó matematikai elvárásától való eltérésének négyzetének matematikai elvárása:

Példa... A fenti példában azt találjuk.

Egy valószínűségi változó matematikai elvárása a következő:

Az eltérés négyzetének lehetséges értékei:

; ;

Az eltérés egyenlő:

A gyakorlatban azonban ez a varianciaszámítási módszer kényelmetlen, mivel nehézkes számításokhoz vezet egy valószínűségi változó nagyszámú értékére. Ezért egy másik módszert alkalmaznak.

Variancia számítása

Tétel. A variancia egyenlő az X valószínűségi változó négyzetének matematikai elvárása és a matematikai elvárás négyzete közötti különbséggel:

Bizonyíték. Figyelembe véve, hogy a matematikai elvárás és a matematikai elvárás négyzete állandó érték, a következőt írhatja:

Alkalmazzuk ezt a képletet a fenti példára:

x
X 2
p	0,0778	0,2592	0,3456	0,2304	0,0768	0,0102

Diszperziós tulajdonságok

1) Egy állandó varianciája nulla:

2) Az állandó tényező a diszperziós előjelből négyzetre emelve vehető ki:

.

3) Két független valószínűségi változó összegének szórása egyenlő ezen értékek szórásának összegével:

4) Két független valószínűségi változó különbségének szórása egyenlő ezen értékek szórásának összegével:

Ennek az egyenlőségnek az érvényessége a 2. tulajdonságból következik.

Tétel. Az A esemény bekövetkezésének számának szórása n független próbában, amelyek mindegyikében az esemény bekövetkezésének valószínűsége állandó, egyenlő a kísérletek számának a bekövetkezési valószínűséggel és a nem bekövetkezési valószínűséggel való szorzatával. az esemény előfordulása az egyes kísérletekben:

Példa. Az üzem az első osztályú cikkek 96%-át és a második osztályú cikkek 4%-át állítja elő. 1000 tétel véletlenszerűen kerül kiválasztásra. Hadd x- az első osztályú termékek száma az adott mintában. Keresse meg egy valószínűségi változó eloszlási törvényét, matematikai elvárását és varianciáját!

Így az eloszlási törvény binomiálisnak tekinthető.

Példa. Határozzuk meg egy diszkrét valószínűségi változó varianciáját x- az esemény előfordulásának száma A két független próbában, ha ennek az eseménynek a valószínűsége minden kísérletben egyenlő, és ismert, hogy

Mivel véletlenszerű érték x binomiális törvény szerint elosztva, akkor

Példa. A független teszteket az esemény bekövetkezésének azonos valószínűségével végezzük A minden tárgyaláson. Keresse meg egy esemény bekövetkezésének valószínűségét A ha egy esemény előfordulási számának szórása három független kísérletben 0,63.

A binomiális törvény varianciájának képlete szerint a következőket kapjuk:

;

Példa. Egy négy, egymástól függetlenül működő eszközből álló eszközt tesztelnek. Az egyes eszközök meghibásodásának valószínűsége rendre ; ; . Határozza meg a meghibásodott eszközök számának matematikai elvárását és szórását!

Ha a meghibásodott eszközök számát valószínűségi változónak vesszük, azt látjuk, hogy ez a valószínűségi változó 0, 1, 2, 3 vagy 4 értéket vehet fel.

Ennek a valószínűségi változónak az eloszlási törvényének elkészítéséhez meg kell határozni a megfelelő valószínűségeket. Fogadjuk el.

1) Egyetlen eszköz sem hibásodott meg:

2) Az egyik eszköz meghibásodott.