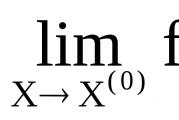Velikost: px

Začít zobrazovat ze stránky:

Přepis

1 Funkce více proměnných 11. Definice funkce více proměnných. Limita a kontinuita FNP 1. Definice funkce několika proměnných DEFINICE. Nechť X \u003d (1 n i X i R) U R. Funkce: X U se nazývá funkce n proměnných. Zapište: u \u003d 1 n, kde zákon stanoví korespondenci mezi 1 n a u. Hodnota u \u003d 1 n pro 1 \u003d 1 \u003d n \u003d n je zapsána ve tvaru u \u003d 1 n nebo u 1 1 n n

2 Název: X doména definice funkce Určete: Du 1 n argumenty nezávislé proměnné U rozsah hodnot Označte: Eu u u závislá proměnná funkce. ZPŮSOBY ÚKOLU FNP 1 slovně; tabelární; 3 analytický: ale explicitní úkol, tj. vzorec u \u003d 1 n b je implicitní úkol, tj. rovnice F 1 n u \u003d. 4 Function \u003d lze nastavit graficky. DEFINICE. Graf funkce \u003d se nazývá lokus bodů v prostoru se souřadnicemi; ; D. Graf funkce \u003d bude také nazýván "povrch \u003d".

3 Úrovňová čára funkce \u003d je lokus bodů roviny, ve které má funkce stejnou hodnotu C. 1 Úrovňová čára je přímka v D, která má rovnici \u003d C. Rovinná čára je promítnutí na rovinu O průsečíku grafu funkce \u003d a roviny \u003d C. C se rovná C1C1 + h C1 + h C1 + nh. Dostáváme vodorovné čáry podle místa, na kterém lze posoudit graf funkce, a tedy povahu změny funkce.

4 Pokud jsou linie „tlustší“, funkce se mění rychleji, plocha představující funkci je strmější.

5 Úrovňový povrch funkce u \u003d je lokus bodů v prostoru O, ve kterém má funkce stejnou hodnotu C. Rovnice hladinového povrchu: \u003d C .. Mez funkce několika proměnných Připomeňme: Číslo AR se nazývá limit funkce, protože funkce má sklon k limitu v bodě, pokud \u003e\u003e tak, že pokud U *, pak UA.

6 O; \u003d \u003d kde DO. ; O u \u003d \u003d kde DO. ; ; Analogicky bude posloupnost 1 n považována za karteziánské souřadnice bodu v n-dimenzionálním prostoru a funkci n proměnných budeme považovat za funkci bodu v tomto prostoru. Označení: R n n-rozměrný prostor u \u003d kde 1 n R n funkce n proměnných.

7 Pokud 1 1 O, pak je vzdálenost mezi nimi označena: 1 je nalezena vzorcem: Pokud O, pak pokud O pak shrneme tyto vzorce, budeme předpokládat, že vzdálenost mezi body v n-dimenzionálním prostoru 1 1 n 1 n R n je rovná n n

8 Nechť 1 n R n. Soubor bodů R n, které jsou umístěny ve vzdálenosti méně od, se bude nazývat - sousednost bodu a označená U. Jinými slovy - sousedství 1 n sestává z bodů 1 n, pro které platí nerovnost 1 1 n n. Pro n \u003d 1 U \u003d (O \u003d< } = +. При n = U { O т.е. U точки круг с центром в точке и радиусом. При n = 3 U { O } т.е. U точки шар с центром в точке и радиусом. }

9 - sousedství bodu R n bez samotného bodu se bude nazývat punktuované a označené U * Nechť je funkce n proměnných u \u003d definována v nějaké sousedství bodu R n, s výjimkou samotné. DEFINICE. Číslo AR se nazývá limit funkce, protože limit funkce má sklon k bodu, pokud \u003e\u003e tak, že pokud U *, pak UA. Napsáno v obecném případě: lim A A пи Pro funkci \u003d: lim A.

10 Poznámky. 1 Podmínka U * znamená, že nerovnost platí: n 1 1 n Podmínka UA znamená, že pro nerovnost A< 3 Так как формально определение предела функции n переменных ничем не отличается от определения предела функции одной переменной то все утверждения которые были получены о пределах функции одной переменной и в которых не используется упорядоченность точек числовой прямой остаются верными и для предела функции n переменных. 4 Определение бесконечно большой функции переносится на случай функции n переменных тоже дословно сформулировать самостоятельно.

11 3. Spojitost funkce více proměnných Nechť u \u003d bude definováno v nějaké sousedství R n. DEFINICE 1. Funkce se nazývá spojitá v bodě, pokud je limita rovnosti pravdivá, nebo jinými slovy, pokud \u003e\u003e tak, že pokud U tj.< то U т.е. <. Справедливы утверждения: 1 арифметические операции над непрерывными в точке функциями приводят к непрерывным в этой точке функциям при условии что деление производится на функцию не обращающуюся в ноль; сложная функция составленная из нескольких непрерывных функций тоже будет непрерывной.

12 Je-li funkce u \u003d definována v určitém sousedství bodu, s výjimkou možná sama o sobě, ale není v tomto bodě spojitá, nazývá se v tomto bodě nespojitá a samotný bod je diskontinuálním bodem. Nechť G je nějaká množina bodů v R n a G. Bod se nazývá vnitřní bod množiny G, pokud U G. Nastavená množina, z níž je vnitřní bod, se nazývá otevřená. Bod se nazývá hraničním bodem množiny G, pokud v kterémkoli z jeho sousedství existují body z G a body, které nepatří k G. Soubor všech hraničních bodů množiny G se nazývá její hranice. Soubor obsahující jeho hranici se nazývá uzavřený.

13 Soubor G se nazývá připojený, pokud lze kterýkoli z jeho bodů spojit spojitou křivkou skládající se z bodů této sady. Komentář. Spojitá křivka v n-rozměrném prostoru je lokusem bodů 1 n, jejichž souřadnice vyhovují rovnicím 1 \u003d 1 t \u003d t n \u003d nt, kde 1 \u003d 1 t \u003d t n \u003d nt jsou spojité funkce parametru t; Připojená otevřená sada se nazývá oblast. Připojená uzavřená sada se nazývá uzavřená oblast. Doména ležící zcela v nějakém sousedství bodu O se nazývá ohraničená.

14 TEOREM analogie Weierstrassovy a Cauchyovy věty pro FNP. Pokud je funkce n proměnných u \u003d spojitá v uzavřené a ohraničené doméně D, pak je ohraničena 1; dosahuje v D svou nejvyšší a nejnižší hodnotu; 3 bere všechny mezilehlé hodnoty mezi libovolnými dvěma z jeho hodnot.

15 1. Částečné deriváty Pro přehlednost budou všechny definice a příkazy formulovány pro funkce proměnných -x nebo 3-proměnných. Přirozeně se zobecňují v případě většího počtu neznámých. Nechte \u003d D \u003d D O D otevřené oblasti. Nechť D. Dáme přírůstek ponechávající hodnotu beze změny, takže bod + D. V tomto případě \u003d obdrží přírůstek \u003d \u003d +. se v bodě nazývá částečný přírůstek funkce \u003d.

16 DEFINICE. Mezní hodnota poměru, pokud existuje a je konečná, se nazývá částečný derivát funkce \u003d s ohledem na proměnnou v bodě. Uveďte: nebo

17 Poznámky. 1 Označení a měla by být chápána jako celé symboly, nikoli jako kvocient dvou veličin. Samostatné výrazy a význam nemají žádný význam. charakterizuje rychlost změny funkce \u003d v bodě fyzického významu parciální derivace s ohledem na. Částečná derivace funkce \u003d s ohledem na proměnnou v bodě je definována podobně: lim lim Označení:

18 Korešpondence je funkce definovaná na D1 D D. Nazývá se parciální derivace funkce \u003d vzhledem k proměnné a je označena. Operace hledání funkce \u003d její parciální derivace se nazývá diferenciace funkce \u003d vzhledem k proměnné, resp. ; ; ; ;. E

19 Ve skutečnosti se jedná o obvyklý derivát funkce \u003d považovaný za funkci jedné proměnné, respektive při konstantní hodnotě druhé proměnné. Proto se výpočet dílčích derivátů provádí podle stejných pravidel jako pro funkci jedné proměnné. V tomto případě je jedna z proměnných považována za konstantu. PŘÍKLAD. Najděte dílčí deriváty s ohledem na funkci \u003d + + 3 as ohledem na ni

20 GEOMETRICKÝ SENSE parciálních derivátů funkce dvou proměnných. Nechť funkce \u003d má částečný derivát s ohledem na. Nechť plocha S je graf funkce \u003d. S P T A Pak tg tg, kde úhel sklonu k ose OO dotyčnice nakreslený v bodě P k průsečíku plochy S a rovině \u003d \u003d. S P K B

Kapitola 5 FUNKCE VÍCENÝCH PROMĚNNÝCH PROSTORŮ Prostor R n Koncept funkce více proměnných Definice Sada všech uspořádaných množin (, n), kde n jsou reálná čísla, se nazývá n-dimenzionální

13. Částečné deriváty vyšších řádů Nechť \u003d mají a jsou definovány v O O. Funkce a nazývají se také částečné deriváty funkce prvního řádu nebo první částečné deriváty funkce. a obecně

Funkce více proměnných Funkce jedné nezávislé proměnné nepokrývají všechny závislosti, které v přírodě existují. Je proto přirozené rozšířit známou koncepci funkční závislosti a zavést ji

M O N Í N Á V A V A B O V A N I I N A U K I R O S I J S K O J F E D E R A T C I FEDERÁLNÍ STAV AUTONOMICKÁ VZDĚLÁVACÍ INSTITUCE VYSOKOŠKOLSKÉHO VZDĚLÁVÁNÍ "Národní výzkum

I Definice funkce několika proměnných Doména definice Při studiu mnoha jevů se musíme zabývat funkcemi dvou nebo více nezávislých proměnných. Například tělesná teplota v daném okamžiku

PŘEDNÁŠKA N9. Funkce několika proměnných. Omezit. Spojitost ... Základní definice a notace ... pojem funkce více proměnných .... 3. Limit funkce více proměnných .... 3 4. Spojitost

Přednášky Kapitola Funkce několika proměnných Základní pojmy Některé funkce několika proměnných jsou dobře známy. Uveďme několik příkladů Pro výpočet oblasti trojúhelníku je znám Heronův vzorec S

Přednáška připravená doc. Musina MV Spojitost funkce Nechť je funkce y \u003d f (x) definována v bodě x a v určitém sousedství tohoto bodu Funkce y \u003d f (x) se nazývá spojitá v bodě x, pokud existuje

FUNKCE MNOŽSKÝCH PROMĚNNÝCH 1. Základní pojmy. Pokud je každé dvojici nezávislých proměnných z nějaké množiny D přiřazeno proměnné množství, nazývá se to funkce dvou

Oddíl 2 Teorie limitů Téma Numerické sekvence Stanovení numerické sekvence 2 Ohraničené a nevázané sekvence 3 Monotonové sekvence 4 Infinitesimální a

Kapitola 3 Funkce více proměnných 1 Základní pojmy Nechť existují n + 1 proměnné 1, n, které jsou vzájemně propojeny tak, že každá sada číselných hodnot proměnných 1, n odpovídá jedinečné

~ 1 ~ FUNKCE VELKÝCH proměnných 3 Funkce dvou proměnných, definice domény, metody definice a geometrický význam. Definice: z f, se nazývá funkce dvou proměnných, pokud každá dvojice hodnot,

44 Příklad Najděte celkový derivát komplexní funkce \u003d sin v cos w, kde v \u003d ln + 1 w \u003d 1 Podle vzorce (9) d v w v w \u003d vw d sin cos + cos cos + 1 sin sin 1 Nyní najděte celkový diferenciál komplexní funkce f

Spojitost funkcí Kontinuita funkce v bodě Jednostranné limity Definice A číslo A se nazývá limit funkce f (x) vlevo, protože x má sklon k a, pokud pro nějaké číslo takové číslo existuje

Gratulujeme k začátku nového školního roku. Přeji vám úspěch ve studiu funkcí mnoha proměnných a diferenciálních rovnic Webová stránka oddělení http://kvm.gubkin.ru 1 Funkce mnoha proměnných 2 Definice

OBSAH ÚVOD 5 Téma DIFERENCIÁLNÍ VÝPOČET FUNKCÍ NĚKTERÝCH PROMĚNNÝCH Přednáškový prostor R 6 Přednáška Limit a kontinuita funkce více proměnných 5 Přednáška 3 Funkce několika proměnných

3. Nekonečně velké sekvence DEFINICE. Numerická sekvence (n) se nazývá nekonečně velká, pokud M\u003e NN je taková, že n\u003e M, n\u003e n. GEOMETRICKÁ INTERPRETACE NEPLATNĚ VELKÉ SEKVENCE

Téma 8 DIFERENCIÁLNÍ VÝPOČET FUNKCÍ NĚKTERÝCH proměnných Přednáška 8.1. Funkce několika proměnných. Parciální derivátový plán 1. Koncept funkce dvou a několika proměnných .. Limit a kontinuita

4. Spojitost funkce 1. Základní definice Nechť f (x) bude definováno v nějaké části bodu x. DEFINICE 1. Funkce f (x) se nazývá spojitá v bodě x, pokud je rovnost f (x) pravdivá. (1)

Sekvence. Definice. Pokud je každé přirozené číslo (N) podle nějakého zákona spojeno s číslem (), pak toto definuje numerickou sekvenci, ... (nebo jen sekvenci).

PŘEDNÁŠKA N33. Složité proměnné funkce. Limity. Kontinuita. Elementární funkce. Diferenciace FKP. Derivační vlastnosti. 1. Posloupnosti komplexních čísel. Limit .... 1.Limited

Matematická analýza Sekce: Úvod do analýzy Téma: Limit funkce Limit funkce a její vlastnosti, nekonečně velké funkce a jejich vlastnosti Přednášející Yanuschik OV 215 g 3 Limit funkce 1 Definice limitu

[definice geometrického znázornění funkce dvou proměnných způsoby definování klasifikace funkcí množin R (n) limit funkce - spojitost věty o spojitých funkcích - příklady] Funkce

Metodické pokyny a varianty RGR na téma Funkce několika proměnných pro studenty oboru Design. Je-li množství jednoznačně určeno určením hodnot veličin a nezávisle na sobě,

Být schopen: Téma 1. Limit a kontinuita funkce Vypočítat limity funkcí a numerické sekvence pomocí různých technik, včetně úžasných limitů, porovnat infinitesimální

Úvod do analýzy funkce několika proměnných L.I. Terekhina, I.I. Oprava funkcí několika proměnných Přednáška 1 Teprve dosud byla podrobně studována teorie funkcí jedné nezávislé proměnné. V realitě

Téma 6. Limity posloupností a funkcí, jejich vlastnosti a aplikace 1 Teorie funkcí více proměnných (argumenty) Diferenciální počet funkcí více proměnných Definice funkce

Diferenciace implicitně definované funkce Zvažte funkci (,) \u003d C (C \u003d const) Tato rovnice definuje implicitní funkci () Předpokládejme, že jsme tuto rovnici vyřešili a našli explicitní výraz \u003d () Nyní můžeme

Lekce 7 Průměrné věty. L'Hôpitalovo pravidlo 7. Střední střední věty Střední střední věty jsou tři věty: Rolle, Lagrange a Cauchy, z nichž každá zobecňuje předchozí. Tyto věty se také nazývají

Praktická lekce Diferenciace komplexní a implikační funkce Diferenciace komplexní funkce Diferenciace implicitní funkce dané jednou rovnicí Systémy implicitní a parametricky dané

Proměnné a stálé hodnoty V důsledku měření fyzických veličin (čas, plocha, objem, hmotnost, rychlost atd.) Se stanoví jejich numerické hodnoty. Math se zabývá veličinami, rozptýlením

Téma Limitní teorie Praktická lekce Číselné sekvence Stanovení číselné sekvence Ohraničené a neohraničené sekvence Monotónní sekvence Infinitesimal

1 Umístění bodů v komplexní rovině Definujme pro funkce dvou reálných proměnných základní geometrické pojmy spojené s umístěním bodů v rovině. Dáme definice

Zkompilován VPBelkin 1 Přednáška 1 Funkce několika proměnných 1 Základní pojmy Závislost \u003d f (1, n) proměnné na proměnných 1, n se nazývá funkce n argumentů 1, n V následujícím textu se budeme zabývat

5 Bod, ve kterém FF F nebo alespoň jeden z těchto derivátů neexistuje, se nazývá singulární bod povrchu. V takovém bodě nemusí mít povrch tangenciální rovinu Definice Normální k povrchu

FUNKCE JEDNÉ proměnné Pojetí funkce Pojetí funkce je spojeno se založením vztahu mezi elementy dvou sad Příklad: Sada přirozených čísel a B sada čtverců přirozených čísel

MoscowÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ Moskevská státní technická univerzita pojmenovaná po N.E. Bauman Fakulta základních věd Katedra matematického modelování À. ». Anatnikov, A.N. Grienko

8 Komplexní numerická řada Zvažte číselnou řadu se složitými čísly tvaru k a, (46), kde (a k) je daná číselná posloupnost s komplexními pojmy k Řada (46) se nazývá konvergentní

Přednáška. Funkční řádky. Definice funkční řady Řada, jejíž členy jsou funkce x, se nazývá funkční: u \u003d u (x) + u + K + u + K \u003d Když x dáme určitou hodnotu x,

PŘEDNÁŠKA 8 Diferenciál funkce v bodě Derivát složené a inverzní funkce Diferenciál funkce v bodě Nechť je funkce f () definována v určité části bodu Pokud lze přírůstek funkce f ()

Přednášky 89 Kapitola 5 Kontinuita funkce 5 Kontinuita funkce v bodě Koncept kontinuity funkce je jedním ze základních konceptů vyšší matematiky. Je zřejmé, že graf spojité funkce je

ŘEŠENÍ TYPICKÝCH PŘÍKLADŮ Najděte doménu D a sadu hodnot E funkce y Řešení Funkce y je definována, pokud jsou ty, pokud Proto je doménou funkce množina f; D R Od

2 2. Metrické prostory Jedním z nejčastějších konceptů v matematice je pojem vzdálenosti. Používá se v analytické geometrii ke studiu vlastností geometrických objektů v euklidu

Samozřejmě, úkol. Dokažte, že Riemannova funkce, pokud 0, m m R (), pokud, m, m 0 a zlomek je neredukovatelný, 0, pokud je iracionální, je nespojitá v každém racionálním bodě a spojitá v každém iracionálním. Rozhodnutí.

Katedra matematiky a informatiky Prvky vyšší matematiky Pedagogicko-metodický komplex pro studenty středních odborných škol s využitím distančních technologií Modul Diferenciální počet Zpracoval:

METODOLOGICKÉ POKYNY PRO VÝPOČTOVÉ PROBLÉMY PRO KURZ VYSOKÝCH MATEMATIKY „ORDINÁRNÍ ROZDĚLENÍ O SÉRII DVOJITÉ INTEGRÁLY“ ČÁST III TÉMA SÉRIE Obsah Série Číselná řada Konvergence a divergence

Ministerstvo školství a vědy Ruské federace Federální státní rozpočet Vzdělávací instituce vysokoškolského vzdělávání "Moskevský letecký institut (národní výzkum)

MoscowÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ Moskevská státní technická univerzita pojmenovaná po N.E. Bauman Fakulta základních věd Katedra matematického modelování À.Í. Santnikov,

Matematická analýza (v.) 1 Číselná řada. 1.1 Koncept řady čísel. Konvergence číselných řad. Definice. Zvažte číselnou posloupnost (a n) a vytvořte výraz tvaru: a 1 + a + ... + a

Koncept komplexní proměnné Limit a kontinuita komplexní proměnné Nechť jsou dány dvě sady komplexních čísel D a Δ a každému číslu z D je přiřazeno číslo ω Δ, které je označeno

ZVLÁŠTNÍ INTEGRÁL. Integrální součty a určitý integrál Nechť je dána funkce y \u003d f (), definovaná v intervalu [, b], kde< b. Разобьём отрезок [, b ] с помощью точек деления на n элементарных

ROZDĚLENÍ FUNKCÍ JEDNÉ proměnné. APLIKACE DERIVATIVA NA STUDIU FUNKCÍ Koncept derivátů a diferenciálů vyšších řádů Derivát f (se nazývá derivát prvního řádu (nebo

10 Zkoumání funkcí a vykreslování grafů 10 Zkoumání funkcí a vytváření grafů 1 Zvyšování a snižování funkce 1 x (1 1 DEFINICE Funkce y \u003d f (x) se nazývá zvyšující se (neklesající)

Přednáška 4 Diferenciální rovnice prvního řádu Obecné pojmy Diferenciální rovnice jsou rovnice, ve kterých nejsou známy funkce jedné nebo více proměnných, a v rovnicích

Otázky k přípravě na zkoušku Téma. Lineární algebra 1. Co je určující? Jaké transformace se nemění určující hodnota? 2. V jakých případech se determinant rovná nule? Co následuje

PŘEDNÁŠKA N Vlastnosti nekonečných a nekonečně velkých funkcí Pozoruhodné limity Kontinuita funkcí Vlastnosti nekonečných kritérií Kritéria pro existenci limitu 3 Vlastnosti nekonečně velkých 4 První

ROZDĚLENÍ FUNKCÍ JEDNÉ proměnné Pojem derivátu, jeho geometrický a fyzický význam Problémy vedoucí k konceptu derivátu Definice tangens S k přímce y f (x) v bodě A x; f (

Lim 3 Diferenciace funkcí 3 Derivace funkce Derivát funkce f v bodě se nazývá následující limit f f df f "d, kde f" a df d notace pro derivaci Operace nalezení derivátu

MoscowÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ Moskevská státní technická univerzita pojmenovaná po N.E. Bauman Fakulta základních věd Katedra matematického modelování À. ». Anatnikov, A.N. Grienko

Matematická analýza Sekce: Integrace FNP Téma: Křivočarý integrál druhého typu Přednášející Pakhomova E.G. 2013 10 10. Křivočarý křivočarý integrál druhého druhu s ohledem na souřadnice

Přednáška 6 1 SA Lavrenchenko Deriváty 1 Definice derivátu Derivace funkce je základní koncept diferenciálního počtu definovaný jako limit rozdílového poměru Definice 11 (derivát

Vykreslovací funkce 1. Plán studia funkce při vytváření grafu 1. Najděte doménu funkce. Často je užitečné zohlednit více hodnot funkce. Prozkoumejte speciální vlastnosti funkce:

ODDÍL 5 Integrální počet funkcí jedné proměnné Materiály připravené učiteli matematiky katedry všeobecného vzdělávání pro systém elektronického distančního vzdělávání Obsah

Přednáška 9. Deriváty a diferenciály vyšších řádů, jejich vlastnosti. Extrémní body funkce. Fermatovy a Rolleovy věty. Nechť je funkce y na některém segmentu [b] diferencovatelná. V tomto případě jeho derivát

Přednáška 5 Deriváty základních elementárních funkcí Abstrakt: Jsou uvedeny fyzikální a geometrické interpretace derivace funkce jedné proměnné. Příklady diferenciace funkce a pravidla

MINISTERSTVO VZDĚLÁVÁNÍ A VĚDY STAV MOSKVA TECHNICKÁ UNIVERZITA „MAMI“ Oddělení „Vyšší matematika“ MA Bodunov, SI Borodina, VV Pokazeev, BE Teush OI Tkachenko, ROZDÍLNÁ VÝPOČET

MINISTERSTVO VZDĚLÁVÁNÍ A VĚDA RUSKÉ FEDERACE GOU VPO „SIBERSKÝ STÁT GEODESICKÁ AKADEMIE“ OG Pavlovskaya EC Plyusnina MATEMATIKA Část Funkce několika proměnných Metodické pokyny

I Sady Základní pojmy Mapování množin Sada je jedním ze základních konceptů matematiky, který není definován. Sada se skládá z prvků Libovolná kolekce prvků libovolného rodu

Pro funkce několika proměnných lze zavést koncepty limitu a kontinuity. Koncepty limitu a kontinuity zavedené dříve pro funkci jedné proměnné jsou zvláštním případem těchto konceptů pro funkce několika proměnných.

Volá se číslo A. funkční limity \u003d f (X)\u003d f (x 1, x 2, ... x n) když X inklinuje k X (0) \u003d (x 1 (0), x 2 (0), ... x n (0)) (nebo v bod X (0) ), jestliže pro nějaké, dokonce libovolně malé kladné číslo, existuje kladné číslo (v závislosti na, tj.  \u003d  ()) takové, že pro všechny body X, které jsou od X (0) odděleny vzdáleností menší než , (s výjimkou snad bodu X (0) , ty. pro) nerovnost je pravdivá: | f (X) - A |<.

Hranice funkce v bodě X (0) je označena
nebo f (X) forА pro XX (0) nebo
.

Číslo A je tedy limitem funkce y \u003d f (X) pro XX (0), pokud pro libovolnou\u003e 0 existuje sousedství bodu X (0) tak, že pro všechny body z tohoto sousedství jsou hodnoty funkce f (X) ) budou uzavřeny v sousedství bodu A na numerické ose hodnot funkcí.

Výpočet limitů funkcí několika proměnných je mnohem komplikovanější než v případě funkcí jedné proměnné. Pokud na přímce existují pouze dva směry, podél nichž se argument může pohybovat k omezujícímu bodu (doprava a doleva), pak v prostorech vyššího rozměru (dokonce i v dvourozměrném prostoru - v rovině) existuje nekonečně mnoho takových směrů a limity funkce v různých směrech se nemusí shodovat ... V některých případech se však takové limity počítají poměrně snadno (například viz Kremerova učebnice, s. 407).

Vyvolá se funkce s více proměnnými nepřetržitýv bodě, pokud je v tomto bodě definován, má konečný limit a tento limit se rovná hodnotě funkce v tomto bodě, tj.
.

Geometrický význam kontinuity funkce dvou proměnných je takový, že graf této funkce je pevný povrch.

Parciální derivace funkcí více proměnných

Vezměte bod X \u003d (x 1, x 2, ... x n). Dejme argument x 1 přírůstek x 1, argument x 2 přírůstek x 2 atd., Argumentu x n přírůstek x n; pak funkce z \u003d f (x) přijme přírůstek z \u003d f (x 1 + x 1, x 2 + x 2, ... x n + x n) -f (X). Toto množství se nazývá plný přírůstekfunkce v bodě X. Pokud nastavíme přírůstek pouze jednoho z argumentů, výsledné přírůstky funkce se nazývají soukromé... Například ,,, jsou soukromé přírůstky.

V obecném případě se úplný přírůstek funkce nerovná součtu kvocientů, i když někdy k této situaci může dojít.

Vyhledejme například kvocienty a celkový přírůstek funkce z \u003d 1 / (x 1 x 2).

Částečný přírůstek argumentem x 1 bude mít podobu:

Částečný přírůstek argumentem x 2 bude mít podobu:

Celý přírůstek se stává:

Lze ukázat, že v tomto příkladu se součet dílčích přírůstků nerovná úplnému přírůstku funkce z:

Parciální derivacefunkce několika proměnných z \u003d f (X) se nazývá limit poměru odpovídajícího částečného přírůstku funkce k přírůstku uvažovaného argumentu, protože tento argument má sklon k nule (pokud tento limit existuje):

Částečný derivát je nebo z / x j.

Z definice dílčích derivátů vyplývá, že k nalezení derivátu z / x j musí být všechny proměnné argumenty považovány za konstantní, s výjimkou jednoho -x j.

Zejména, pokud z je funkce dvou proměnných x a y (z \u003d f (x, y)), pak její částečná derivace vzhledem k x je
a pro jeho nalezení musí být argument y považován za konstantní. Částečná derivace z se rovná
a pro jeho nalezení musí být argument x považován za konstantní.

Vyhledejme například částečné deriváty následujících funkcí:

Příklad 1.z \u003d xlny + y / x

Pro nalezení parciální derivace vzhledem k x považujeme y za konstantu. Potom z x "\u003d lny * (x)" + y * (1 / x) "\u003d lny + y * (- 1) * x -2 \u003d lny - y / (x 2).

Podobně rozlišujeme tuto funkci s ohledem na y za předpokladu, že x je konstanta: z y "\u003d x (lny)" + (1 / x) * (y) "\u003d x / y + 1 / x

Příklad 2.z \u003d x y

Částečný derivát vzhledem k x je derivát výkonové funkce, tj. z x "\u003d yx y -1.

Částečný derivát vzhledem k y je derivát exponenciální funkce, tj. Z y "\u003d x y lnx.

Koncept částečného derivátu má velmi jasný ekonomický význam. Protože funkce několika proměnných v ekonomii vyjadřují závislost určité veličiny na několika dalších faktorech (někdy včetně času), působí parciální derivát jako rychlost změny této veličiny v čase nebo ve vztahu k jinému studovanému faktoru, pokud se ostatní faktory nezmění.

Předpokládejme například, že obchod prodává zmrzlinu - krémovou za 25 rublů. za kus, čokoláda 30 rublů. za kus a pistácie pro 32 rublů. kus. Označme x 1 - objem prodeje zmrzliny (ks), X 2 - objem prodeje zmrzliny čokolády (ks), X 3 - objem prodeje zmrzliny pistácie (ks). Potom lze tržby z (rublů) z prodeje těchto druhů zmrzliny vypočítat pomocí funkce tří proměnných z \u003d 25x 1 + 30x 2 + 32x 3. Najdeme částečnou derivaci této funkce s ohledem na x 1: \u003d 25. Jaký je ekonomický význam této hodnoty? Ukazuje, jak moc se příjmy zvýší jedinou změnou v prodeji zmrzliny, za předpokladu, že prodej ostatních druhů zmrzliny zůstane na stejné úrovni. Jinými slovy, jedná se o míru změny celkových příjmů v poměru ke změně prodeje zmrzliny. Podobné zdůvodnění lze provést u obou ostatních proměnných.

Výše uvedený pojem částečného derivátu se týká částečný derivát prvního řádu... Představme si koncepty dílčích derivátů vyššího řádu.

Pokud jsou dílčími deriváty prvního řádu diferencovatelné funkce, pak můžeme najít jejich dílčí deriváty, které se nazývají částečné deriváty druhého řádu:
... Částečné deriváty druhého řádu lze použít k výpočtu dílčích derivátů třetího řádu atd.

Je možné prokázat, že pokud jsou částečné derivace funkce z \u003d f (x, y) druhého řádu spojité v určitém bodě, pak v tomto bodě
.

KAPITOLA III. Funkce několika proměnných §11. Definování funkce několika proměnných. Limita a kontinuita FNP 1. Definice funkce několika proměnných DEFINICE. Nechť X \u003d ((x 1, x 2, ..., x n) | x i X i), U. Funkce f: X U se nazývá funkce n proměnných. Zapište: u \u003d f (x 1, x 2, ..., x n), kde f je zákon, který definuje korespondenci mezi x 1, x 2,…, x n a u. Hodnota u \u003d f (x 1, x 2, ..., xn) pro x 1 \u003d x 01, x 2 \u003d x 02, ..., xn \u003d x 0n je zapsána jako u \u003d f (x 01, x 02, ..., x 0n) nebo

Nazývají se: X - doména funkce (Označení: D (u)), x 1, x 2, ..., xn - argumenty (nezávislé proměnné), U - rozsah hodnot (Označení: E (u)), u (u U) - závislá proměnná (funkce). ZPŮSOBY PŘIDĚLOVÁNÍ FNP 1) ústní; 2) tabulární; 3) analytické: a) explicitní přiřazení (tj. Vzorcem u \u003d f (x 1, x 2, ..., xn)) b) implicitní přiřazení (tj. Rovnicí F (x 1, x 2, ..., xn) , u) \u003d 0). 4) Funkce z \u003d f (x, y) lze nastavit graficky. DEFINICE. Graf funkce z \u003d f (x, y) je lokus bodů v prostoru se souřadnicemi (x; y; f (x, y)), (x, y) D (z). Graf funkce z \u003d f (x, y) bude také nazýván „povrch z \u003d f (x, y)“.

Úrovňový řádek funkce z \u003d f (x, y) je lokusem bodů (x, y) roviny, ve které má funkce stejnou hodnotu C. 1) Úrovňový řádek je přímkou \u200b\u200bv D (z), která má rovnici f ( x, y) \u003d C. 2) Rovinná čára je projekce na rovinu xOy přímky průsečíku grafu funkce z \u003d f (x, y) a roviny z \u003d C. Nastavili jsme C rovné C1, C1 + h, C1 + 2h, ..., C1 + nh. Dostáváme rovné čáry, podle místa, na kterém lze posoudit graf funkce a následně povahu změny funkce.

Hladinový povrch funkce u \u003d f (x, y, z) je geometrické místo bodů v prostoru Oxyz, ve kterém funkce nabývá stejné hodnoty C. Rovnice hladinového povrchu: f (x, y, z) \u003d C. 2. Limit funkce několika proměnných Připomeňme: Číslo A se nazývá limit funkce f (x), protože x má sklon k x 0 (limit funkce f (x) v bodě x 0), pokud\u003e 0\u003e 0 tak, že pokud x U * (x 0, ), poté f (x) U (A,). 0\u003e 0, takže pokud x U * (x 0,), pak f (x) U (A,). "\u003e

(x, y) M xOy; z \u003d f (x, y) \u003d f (M), kde M D xOy. (x, y, z) M Oxyz u \u003d f (x, y, z) \u003d f (M), kde M Oxyz. Analogicky bude posloupnost (x 1, x 2, ..., x n) považována za karteziánské souřadnice bodu v n-dimenzionálním prostoru a bude považovat funkci n proměnných za funkci bodu v tomto prostoru. Označme: n - n-rozměrný prostor, u \u003d f (M), kde M (x 1, x 2, ..., x n) n - funkce n proměnných.

Jestliže M 1 (x 1), M 2 (x 2) Ox, pak vzdálenost mezi nimi (označená: | M 1 M 2 |) se najde podle vzorce: Pokud M 1 (x 1, y 1), M 2 ( x 2, y 2) xOy, pak Pokud M 1 (x 1, y 1, z 1), M 2 (x 2, y 2, z 2) Oxyz, pak zobecnění těchto vzorců, budeme předpokládat, že vzdálenost mezi body n - rozměr M 1 (x 1, x 2, ..., xn), M 2 (y 1, y 2,…, yn) n je

Nechť M 0 (x 01, x 02, ..., x 0n) n. Soubor bodů n, které jsou umístěny ve vzdálenosti menší od M 0, se bude nazývat-sousedství bodu M 0 a bude označeno U (M 0,). Jinými slovy - sousedství M 0 (x 01, x 02, ..., x 0n) sestává z bodů M (x 1, x 2, ..., xn), pro které platí nerovnost Pro n \u003d 1 U (M 0, ) \u003d (M Ox | | M 0 M | \u003d | x - x 0 |

Sousedství bodu M 0 n bez samotného bodu M 0 se nazývá propíchnuté a označené U * (M 0,) Nechť je funkce n proměnných u \u003d f (M) definována v nějaké sousedství bodu M 0 n, s výjimkou snad samotného MO. DEFINICE. Číslo A se nazývá limit funkce f (M), protože M má sklon k M 0 (limit funkce f (M) v bodě M 0), pokud\u003e 0\u003e 0 tak, že pokud MU * (M 0,), pak f (M) U (A,). Obecně uveďte: Pro funkci z \u003d f (x, y): 0\u003e 0, takže pokud M U * (M 0,), pak f (M) U (A,). Obecně uveďte: Pro funkci z \u003d f (x, y): "\u003e

Poznámky. 1) Podmínka M U * (M 0,) znamená, že nerovnost platí: 2) Podmínka f (M) U (A,) znamená, že pro f (M) nerovnost | f (M) - A |

0\u003e 0 tak, že pokud M U (M 0,) "title \u003d" (! LANG: 3. Spojitost funkce více proměnných Nechť u \u003d f (M) je definováno v nějaké sousedství M 0 n. DEFINICE 1. Funkce f (M) se nazývá spojitá v bodě M 0, pokud platí rovnost, jinými slovy, pokud\u003e 0\u003e 0 tak, že pokud M U (M 0,)" class="link_thumb"> 12 !} 3. Spojitost funkce více proměnných Nechť u \u003d f (M) je definováno v nějaké sousedství M 0 n. DEFINICE 1. Funkce f (M) se nazývá spojitá v bodě M 0, pokud platí rovnost, jinými slovy, pokud\u003e 0\u003e 0 tak, že pokud M U (M 0,) (tj. | MM 0 | 0\u003e 0 takový , co když M U (M 0,) "\u003e 0\u003e 0 tak, že pokud M U (M 0,) (tj. | MM 0 | 0\u003e 0 tak, že pokud M U (M 0,)" title \u003d " (! LANG: 3. Spojitost funkce více proměnných. Nechť u \u003d f (M) je definováno v nějaké sousedství M 0 n. DEFINICE 1. Funkce f (M) se nazývá spojitá v bodě M 0, pokud je rovnost pravdivá, jinými slovy, pokud\u003e 0 \u003e 0, takže pokud M U (M 0,)"> title="3. Spojitost funkce více proměnných Nechť u \u003d f (M) je definováno v nějaké sousedství M 0 n. DEFINICE 1. Funkce f (M) se nazývá spojitá v bodě M 0, pokud platí rovnost, nebo jinými slovy, pokud\u003e 0\u003e 0 tak, že pokud M U (M 0,)">!}

Pokud je funkce u \u003d f (M) definována v určitém sousedství bodu M 0 (s výjimkou snad samotného M 0), ale není v tomto bodě spojitá, nazývá se diskontinuální v bodě M 0 a samotný bod MO je bod zlomu. Nechť G je nějaká množina bodů v n a M 0 G. Bod M 0 se nazývá vnitřní bod množiny G, jestliže U (M 0,) G. Sada, jejíž vnitřní bod je nazýván otevřený. Bod M 0 se nazývá hraničním bodem množiny G, pokud některá z jeho sousedství obsahuje jak body z G, tak i body, které nepatří k G. Soubor všech hraničních bodů množiny G se nazývá její hranice. Soubor obsahující jeho hranici se nazývá uzavřený.

Sada G se nazývá připojená, pokud lze kterýkoli z jejích bodů spojit spojitou křivkou skládající se z bodů této sady. Komentář. Spojitá křivka v n-dimenzionálním prostoru je lokusem bodů M (x 1, x 2, ..., xn), jejichž souřadnice vyhovují rovnicím x 1 \u003d x 1 (t), x 2 \u003d x 2 (t), ..., xn \u003d xn (t), kde x 1 \u003d x 1 (t), x 2 \u003d x 2 (t),…, xn \u003d xn (t) jsou spojité funkce parametru t (;). Připojená otevřená sada se nazývá oblast. Připojená uzavřená sada se nazývá uzavřená oblast. Doména, která zcela leží v nějakém sousedství bodu O (0,0, ..., 0), se nazývá ohraničená.

THEOREM (analogie Weierstrassovy a Cauchyovy věty pro FNP). Pokud je funkce n proměnných u \u003d f (M) spojitá v uzavřené a ohraničené doméně D, pak je 1) ohraničena; 2) dosahuje nejvyšší a nejnižší hodnoty v D; 3) vezme všechny mezilehlé hodnoty mezi kterýmikoli dvěma ze svých hodnot.

§12. Částečné deriváty Pro větší přehlednost budou všechny definice a příkazy formulovány pro funkci 2 (nebo 3) proměnných. Přirozeně se zobecňují v případě většího počtu neznámých. Nechť z \u003d f (x, y), D (z) \u003d D xOy, D je otevřená oblast. Nechť M 0 (x 0, y 0) D. Dej x 0 přírůstek x, ponecháme hodnotu y 0 beze změny (takže bod M (x 0 + x, y 0) D). V tomto případě z \u003d f (x, y) obdrží přírůstek x z (M0) \u003d f (M) - f (M0) \u003d f (x 0 + x, y 0) - f (x 0, y 0). x z (M 0) se nazývá částečný přírůstek funkce z \u003d f (x, y) vzhledem k x v bodě M 0 (x 0, y 0).

Poznámky. 1) Označení a je třeba je chápat jako celé symboly, a ne jako kvocient dvou veličin. Samostatné výrazy z (x 0, y 0) a x nedávají smysl. 2) charakterizuje rychlost změny funkce z \u003d f (x, y) vzhledem k x v bodě M0 (x 0, y 0) (fyzikální význam částečného derivátu vzhledem k x). Parciální derivace funkce z \u003d f (x, y) vzhledem k proměnné y v bodě M 0 (x 0, y 0) je definována podobně:

Korelace je funkce definovaná na D1 (D2) D (f). Nazývá se parciální derivace funkce z \u003d f (x, y) vzhledem k proměnné x (y) a je označena. Operace hledání jejích parciálních derivací pro funkci z \u003d f (x, y) se nazývá diferenciace funkce z \u003d f (x, y) vzhledem k proměnné x a y.

Ve skutečnosti je to obyčejný derivát funkce z \u003d f (x, y), považovaný za funkci jedné proměnné x (respektive y) s konstantní hodnotou druhé proměnné. Proto se výpočet dílčích derivátů provádí podle stejných pravidel jako pro funkci jedné proměnné. V tomto případě je jedna z proměnných považována za konstantní. PŘÍKLAD. Najděte dílčí deriváty v x a y funkce f (x, y) \u003d x 2 + xy 2 + y 3

GEOMETRICKÝ SENSE parciálních derivátů funkce dvou proměnných. Nechť funkce z \u003d f (x, y) má parciální derivaci vzhledem k x v M 0 (x 0, y 0). Nechť plocha S je graf funkce z \u003d f (x, y). Potom kde je úhel sklonu k ose Ox tečny nakreslený v bodě P 0 (x 0, y 0, f (x 0, y 0)) k průsečíku plochy S a rovině y \u003d y 0.

Spojitost funkce několika proměnných

Představme si důležitý pomocný koncept - koncept sousedství daného bodu.

Sousedství poloměr r body M 0 (x 0 , v 0) je sada všech bodů ( x, v) uspokojení nerovnosti, tj. soubor všech bodů ležících uvnitř kruhu o poloměru r vystředěný v bodě M 0 (x 0 , v 0).

Pokud řekneme, že funkce f(x, v) má nějakou vlastnost «poblíž bodu ( x 0 , v 0) "nebo" v blízkosti bodu ( x 0 , v 0) ", pak tímto máme na mysli, že existuje takový kruh se středem ( x 0 , v 0), ve všech bodech, ve kterých má tato funkce uvedenou vlastnost.

Před zvážením pojmu kontinuita funkce více proměnných se podívejme na koncept limitu funkce několika proměnných.

Vzhledem k funkci

z = f(x, v),

Definice 4. Číslo A nazvaný limit funkce f(x, v) při pokusu M(x, v) do té míry M 0 (x 0 , v 0) pokud pro každé číslo e\u003e 0 takové číslo existuje r \u003e 0, což pro všechny body M(x, v) pro kterou platí nerovnost, nerovnost

.

Pokud je číslo A je limit funkce f(x, v) v M(x, v) ® M 0 (x 0 , v 0), pak píšou

.

Definice 5. Ať bod M 0 (x 0 , v 0) patří do domény funkce f(x, v) Funkce z \u003d f(x, v) se v tomto okamžiku nazývá kontinuální M 0 (x 0 , v 0) pokud je rovnost

, (2)

a melancholie M(x, v) má sklon k věci M 0 (x 0 , v 0) libovolným způsobem, zatímco zůstane v doméně funkce.

Pokud to označíme x \u003d x 0 + D x, v = v 0 + D v, lze rovnost (2) přepsat takto:

(3)

My označujeme ... Když D x ® 0 a D v ® 0 Dr ® 0, a naopak, pokud Dr ® 0, pak D x ® 0 a D v ® 0.

Je volána funkce, která je spojitá v každém bodě určité oblasti nepřetržitě v terénu.

Pokud v určitém okamžiku N(x 0 , v 0) podmínka (2) není splněna, pak bod N(x 0 , v 0) se nazývá diskontinuitní bod funkce z \u003d f(x, v) Podmínka (3) nemusí být splněna například v následujících případech:

1) z \u003d f(x, v) je definována ve všech bodech některé čtvrti N(x 0 , v 0), s výjimkou vlastního bodu N(x 0 , v 0);

2) funkce z \u003d f(x, v) je definována ve všech bodech okolí bodu N(x 0 , v 0), ale není tam žádný limit;

3) funkce je definována ve všech bodech okolí N(x 0 , v 0) a existuje limit, ale .

Příklad 12. Funkce z = x 2 + v 2 je spojitá pro jakékoli hodnoty x a v, tj. kdekoli v letadle Ooh.

Opravdu, bez ohledu na čísla x a v, D x a D v, my máme

proto,.

Uveďme příklad nespojité funkce.

Příklad 13. Funkce je definována všude kromě bodu x = 0, v = 0.

Zvažte hodnoty z po přímce y \u003d kx (k \u003d const). Je zřejmé, že v tomto směru

,

ty. funkce z podél libovolné přímky procházející počátkem si zachovává konstantní hodnotu v závislosti na sklonu k rovný. Proto, přibližujeme-li se k počátku podél různých cest, získáme různé limitující hodnoty, což znamená, že funkce f(x, v) nemá žádný limit, když bod ( x, v) na povrchu Ooh má sklon k původu. V tomto bodě je tedy funkce nespojitá. Tuto funkci nelze na počátku rozšířit, aby se stala spojitou. Na druhé straně je snadno vidět, že v jiných bodech je tato funkce spojitá.

Označme některé důležité vlastnosti funkce několika proměnných, které jsou spojité v uzavřené a ohraničené doméně. Tyto vlastnosti jsou podobné vlastnostem spojité funkce jedné proměnné v intervalu.

Vlastnost 1... Pokud funkce f(x, v, ...) je definována a spojitá v uzavřené a ohraničené doméně D, pak v oblasti D existuje alespoň jeden bod N(x 0 , v 0, ...) tak, že pro všechny ostatní body regionu vztah

f(x 0 , v 0 , …) ³ f(x, v, …),

a alespoň jeden bod R(x 1 , v 1, ...) tak, že pro všechny ostatní body regionu vztah

f(x 1 , v 1, ...) £ f(x, v, …).

Funkční hodnota f(x 0 , v 0 , …) = M zavolá největší hodnota funkce f(x, v,…) V oblasti Da hodnotu f(x 1 , v 1 , …) = t – nejmenší hodnota.

Tato vlastnost je formulována následovně. Nepřetržitá funkce v uzavřené ohraničené oblasti D dosáhne alespoň jednou nejvyšší hodnoty M a nejmenší hodnota t.

Vlastnost 2. Pokud funkce f(x, v, ...) je spojitá v uzavřené a ohraničené oblasti D a pokud M a t - největší a nejmenší funkční hodnoty f(x, v, ...) v doméně, pak pro libovolné číslo m splňující podmínku t < m < M, v regionu je takový bod R *(x * , v *, ...) že rovnost f(x * , v *, ...) \u003d m.

Důsledek vlastnictví 2. Pokud je funkce f(x, v, ...) je spojitá v uzavřené ohraničené oblasti a má kladné i záporné hodnoty, pak uvnitř oblasti jsou body, ve kterých funkce f(x, v,…) Vanishes.