SYSTÉM DOMÁCÍCH LINEÁRNÍCH ZAŘÍZENÍ

Systém homogenních lineárních rovnic je systém formy

Je jasné, že v tomto případě od té doby všechny prvky jednoho ze sloupců v těchto kvalifikátorech jsou rovny nule.

Vzhledem k tomu, neznámé se nacházejí ve vzorcích , pak v případě, kdy Δ ≠ 0, má systém jedinečné řešení nuly x = y = z \u003d 0. Avšak v mnoha problémech je zajímavá otázka, zda homogenní systém má jiná řešení než nula.

Teorém. Aby systém lineárních homogenních rovnic měl nenulové řešení, je nezbytné a dostatečné, aby Δ ≠ 0.

Pokud tedy determinant Δ ≠ 0, pak má systém jedinečné řešení. Pokud Δ ≠ 0, pak systém lineárních homogenních rovnic má nekonečnou sadu řešení.

Příklady.

Vlastní vektory a vlastní hodnoty matice

Nechť je dána čtvercová matice , X - nějaký sloupec matice, jehož výška se shoduje s řádem matice A. .

V mnoha problémech je třeba vzít v úvahu rovnici s ohledem na X

kde λ je nějaké číslo. Je zřejmé, že pro všechny λ má tato rovnice nulové řešení.

Je voláno číslo λ, pro které má tato rovnice nenulové řešení vlastní význam matice A, a X pro takový λ se nazývá vlastní vektor matice A.

Najděte vlastní vektor matice A... Pokud E∙X \u003d X, lze maticovou rovnici přepsat jako nebo ... V rozšířené podobě lze tuto rovnici přepsat jako systém lineárních rovnic. Opravdu .

A proto

Dostali jsme tedy systém homogenních lineárních rovnic pro určování souřadnic x 1, x 2, x 3 vektor X... Aby systém měl nenulová řešení, je nezbytné a dostatečné, aby determinant systému byl roven nule, tj.

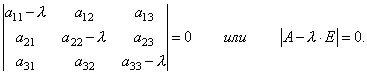
Toto je rovnice 3. stupně v λ. Jmenuje se to charakteristická rovnice matice A a slouží k určení vlastních čísel λ.

Každá vlastní hodnota λ odpovídá vlastnímu sektoru X, jejichž souřadnice jsou určeny ze systému na odpovídající hodnotě λ.

Příklady.

VECTOR ALGEBRA. KONCEPCE VEKTORU

Při studiu různých oborů fyziky existují veličiny, které jsou zcela určeny uvedením jejich číselných hodnot, například délky, plochy, hmotnosti, teploty atd. Nazývají se skalární hodnoty. Kromě nich však existují i \u200b\u200bveličiny, pro jejichž stanovení je kromě numerické hodnoty nutné znát také jejich směr v prostoru, například sílu působící na tělo, rychlost a zrychlení těla, když se pohybuje v prostoru, sílu magnetického pole v daném bodě v prostoru a atd. Taková množství se nazývají vektor.

Představme přísnou definici.

Směrový segment nazvěme segment, vzhledem k jeho koncům, o nichž je známo, který z nich je první a který je druhý.

Vektor se nazývá směrovaný segment, který má určitou délku, tj. je to segment určité délky, ve kterém je jeden z jeho omezujících bodů považován za začátek a druhý za konec. Pokud A - začátek vektoru, B - jeho konec, pak je vektor označen symbolem, navíc je vektor často označován jedním písmenem. Na obrázku je vektor označen úsečkou a jeho směr šipkou.

Modul nebo délka vektor je délka směrového segmentu, který jej definuje. Je označeno || nebo ||.

Takzvaný nulový vektor, jehož začátek a konec se shodují, bude také označován jako vektory. Je to uvedeno. Nulový vektor nemá jednoznačný směr a jeho modul se rovná nule || \u003d 0.

Vektory a jsou nazývány kolineárnípokud jsou umístěny na stejné nebo paralelní linii. Navíc, pokud vektory a jsou ve stejném směru, budeme psát opačně.

Nazývají se vektory umístěné na přímkách rovnoběžných se stejnou rovinou koplanár.

Dva vektory se nazývají rovnat sepokud jsou kolineární, stejně zaměřené a stejně dlouhé. V tomto případě napište.

Z definice rovnosti vektorů vyplývá, že vektor může být přenesen rovnoběžně se sebou samým, přičemž jeho původ je umístěn v kterémkoli místě v prostoru.

například.

LINEÁRNÍ OPERACE NA VEKTORECH

1. Násobení vektoru číslem.

   Produkt vektoru číslem λ je nový vektor takový, že:

   Produkt vektoru s číslem λ je označen.

   

   Například, je vektor namířený ve stejném směru jako vektor a mající délku poloviny délky vektoru.

   Zavedená operace má následující vlastnosti:

2. Přidání vektorů.

   Dovolit a být dva libovolné vektory. Vezměte libovolný bod Ó a konstruovat vektor. Poté, od okamžiku A zrušil vektor. Je volán vektor spojující začátek prvního vektoru s koncem druhého součet těchto vektorů a označených .

   

   Nazývá se formulovaná definice přidání vektoru pravidlo rovnoběžníku, protože stejný součet vektorů lze získat následujícím způsobem. Odložte stranou Ó vektory a. Postavme na těchto vektorech rovnoběžník OABS... Vzhledem k tomu, vektory, vektor, který je úhlopříčka rovnoběžníku nakreslena z vrcholu Ó, bude to samozřejmě součet vektorů.

   

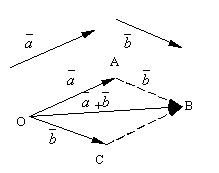
   Je snadné zkontrolovat následující vektorové adiční vlastnosti.

3. Rozdíl vektorů.

   Je volán vektor kolineární k danému vektoru, který má stejnou délku a protisměrně směrovaný naproti vektor pro vektor a je označen. Opačný vektor lze považovat za výsledek vynásobení vektoru číslem λ \u003d –1 :.

Vlastní hodnoty (čísla) a vlastní vektory.
Příklady řešení

Buď sám sebou

Z obou rovnic vyplývá, že.

Pojďme tedy: .

Jako výsledek: Je druhým vlastním vektorem.

Zopakujme důležité body řešení:

- výsledný systém má jistě obecné řešení (rovnice jsou lineárně závislé);

- vybereme „hru“ tak, aby byla celá a první „x“ souřadnice je celá, pozitivní a co možná nejmenší.

- zkontrolujte, zda konkrétní řešení vyhovuje každé rovnici systému.

Odpovědět .

Bylo zde dost mezilehlých „kontrolních bodů“, proto je kontrola rovnosti v zásadě zbytečná.

V různých zdrojích informací jsou souřadnice vlastních vektorů často psány nikoli do sloupců, ale například do řádků: (a abych byl upřímný, jsem zvyklý psát je v řádcích sám)... Tato možnost je přijatelná, ale s ohledem na dané téma lineární transformace technicky pohodlnější použití sloupcové vektory.

Možná se vám zdálo řešení velmi dlouhé, ale to je jen proto, že jsem se k prvnímu příkladu podrobně vyjádřil.

Příklad 2

Matice

Cvičíme sami! Přibližný příklad dokončení úkolu na konci lekce.

Někdy je vyžadován další úkol, jmenovitě:

napsat rozklad kanonické matice

Co to je?

Pokud se vlastní vektory maticové formy základ, pak to může být reprezentováno jako:

Kde je matice složená ze souřadnic vlastních vektorů, - úhlopříčka matice s odpovídajícími vlastními hodnotami.

Takový maticový rozklad se nazývá kanonický nebo úhlopříčka.

Zvažte matici prvního příkladu. Jeho vlastní vektory lineárně nezávislý (non-kolineární) a tvoří základ. Vytvořme matici z jejich souřadnic:

Na hlavní úhlopříčka matice v příslušném pořadí lokalizovány jsou vlastní hodnoty a zbývající prvky jsou rovny nule:
- ještě jednou zdůrazňuji důležitost řádu: „dva“ odpovídá 1. vektoru, a proto je umístěn v 1. sloupci „tři“ - 2. vektoru.

Podle obvyklého algoritmu hledání inverzní matice nebo gauss-Jordanova metodanalézt ... Ne, to není překlep! - před vámi je vzácná událost, jako je zatmění Slunce, když se inverze shodovala s původní maticí.

Zbývá napsat kanonický rozklad matice:

Systém lze řešit pomocí elementárních transformací a v následujících příkladech tuto metodu použijeme. Metoda „školy“ však funguje mnohem rychleji. Z 3. rovnice budeme vyjadřovat: - ve druhé rovnici nahradíme:

Protože první souřadnice je nula, získáme systém, z každé rovnice, která z toho vyplývá.

A znovu dávejte pozor na povinnou přítomnost lineární závislosti... Pokud dostanete pouze triviální řešení , pak bylo správné číslo nalezeno nesprávně nebo byl systém zkompilován / vyřešen s chybou.

Kompaktní souřadnice dávají smysl

Vlastní sektor:

A ještě jednou - zkontrolujeme, že nalezené řešení splňuje každou rovnici systému... V následujících odstavcích a při následných úkolech doporučuji toto přání brát jako povinné pravidlo.

2) Pro vlastní hodnotu podle stejného principu získáme následující systém:

Z 2. rovnice systému vyjadřujeme: - náhrada ve třetí rovnici:

Protože souřadnice "zeta" se rovná nule, dostaneme systém, z každé rovnice, z níž vychází lineární závislost.

Nech být

Prověřujeme to řešení splňuje všechny rovnice v systému.

Vlastní sektor tedy:

3) A konečně, systém odpovídá vlastní hodnotě:

Druhá rovnice vypadá nejjednodušší, takže z ní vyjadřujeme a nahrazujeme ji do 1. a 3. rovnice:

Všechno je v pořádku - vznikl lineární vztah, který nahradíme výrazem:

Výsledkem bylo, že "x" a "igrek" byly vyjádřeny prostřednictvím "z" :. V praxi není nutné takové vztahy dosahovat, v některých případech je vhodnější vyjádřit se skrz nebo skrz. Nebo dokonce „malý vlak“ - například „X“ až „igrek“ a „igrek“ prostřednictvím „z“

Předpokládejme tedy:

Zkontrolujeme, že nalezené řešení splňuje každou rovnici systému a zapíše třetí vlastní vektor

Odpovědět: vlastní vektory:

Geometricky tyto vektory definují tři různé prostorové směry ("Tam a zase zpátky")kterými lineární transformace transformuje nenulové vektory (vlastní vektory) na vektory kolineární k nim.

Pokud je podmínka nutná k nalezení kanonického rozkladu, je to možné zde, protože různé vlastní hodnoty odpovídají různým lineárně nezávislým vlastním vektorům. Skládání matice z jejich souřadnic, diagonální matice z příslušné vlastní hodnoty a najít inverzní matice .

Pokud, podle podmínek, musíte napsat matice lineární transformace na bázi vlastních vektorů, pak odpovíme ve formě. Rozdíl je a rozdíl je významný! Pro tuto matici je matice „de“.

Problém s jednoduššími výpočty pro nezávislé řešení:

Příklad 5

Najděte vlastní vektory lineární transformace dané maticí

Při hledání vlastních čísel zkuste nepřivést záležitost k polynomu 3. stupně. Kromě toho se vaše systémová řešení mohou lišit od mých řešení - není zde jednoznačnost; a vektory, které najdete, se mohou lišit od vzorků vektorů až do proporcionality jejich příslušných souřadnic. Například, a. Je estetičtější představit odpověď ve formě, ale je v pořádku, pokud se zastavíte u druhé možnosti. Však existují rozumné limity, verze už nevypadá moc dobře.

Přibližný konečný vzorek úkolu na konci lekce.

Jak vyřešit problém v případě více vlastních čísel?

Obecný algoritmus zůstává stejný, ale má své vlastní zvláštnosti a je vhodné udržovat některé části řešení v přísnějším akademickém stylu:

Příklad 6

Najděte vlastní čísla a vlastní vektory

Rozhodnutí

Samozřejmě, že kapitalizujeme první báječný sloupec:

A po faktoringu čtvercového trojice:

Výsledkem je získání vlastních čísel, z nichž dvě jsou násobky.

Podívejme se na vlastní vektory:

1) Osamělým vojákem budeme jednat podle „zjednodušeného“ schématu:

Z posledních dvou rovnic je jasně viditelná rovnost, která by samozřejmě měla být nahrazena do 1. rovnice systému:

Není lepší kombinace:
Vlastní sektor:

2-3) Nyní zastřelte několik strážných. V tomto případě se to může ukázat buď dva, nebo jeden vlastní vektor. Bez ohledu na mnohočetnost kořenů nahradíme hodnotu do determinantu což nám přináší následující homogenní systém lineárních rovnic:

Vlastní vektory jsou přesně vektory
základní rozhodovací systém

Ve skutečnosti jsme se celou lekci zabývali pouze hledáním vektorů základního systému. Prozatím nebyl tento termín vyžadován. Mimochodem, ti chytrí studenti, kteří vklouzli tématu do maskovacích kabátů homogenní rovnicebude nucen ji sníst hned.

Jedinou akcí bylo smazat další řádky. Výsledkem je matice jeden po druhém s formálním „příčím“ uprostřed.
- základní proměnná, - volné proměnné. Existují tedy dvě volné proměnné, vektory základního systému jsou také dva.

Pojďme vyjádřit základní proměnnou z hlediska volných proměnných :. Nulový faktor před "x" mu umožňuje vzít absolutně jakékoli hodnoty (což je jasně vidět ze soustavy rovnic).

V kontextu tohoto problému je vhodnější napsat obecné řešení nikoli do řádku, ale do sloupce:

Vlastní vektor odpovídá dvojici:
Dvojice má svůj vlastní vektor:

Poznámka : sofistikovaní čtenáři si mohou vybrat tyto vektory a ústně - pouze analýzou systému , ale tady je potřeba nějaká znalost: existují tři proměnné, pozice matice systému - jednotka, což znamená základní rozhodovací systém sestává z 3 - 1 \u003d 2 vektory. Nalezené vektory jsou však dokonale viditelné i bez těchto znalostí, čistě na intuitivní úrovni. V tomto případě bude třetí vektor zapsán ještě „krásněji“: Varuji vás však, že v jiném příkladu nemusí být jednoduchý výběr, proto je vyloučení odpovědnosti určeno zkušeným lidem. Kromě toho, proč ne, řekněme, jako třetí vektor? Koneckonců, jeho souřadnice také uspokojují každou rovnici systému a vektory jsou lineárně nezávislé. Tato možnost je v zásadě vhodná, ale „zakřivená“, protože „jiný“ vektor je lineární kombinací vektorů základního systému.

Odpovědět: vlastní čísla :, vlastní vektory:

Podobný příklad samostatného řešení:

Příklad 7

Najděte vlastní čísla a vlastní vektory

Hrubý příklad dokončení na konci lekce.

Je třeba poznamenat, že v 6. i 7. příkladu se získá trojice lineárně nezávislých vlastních vektorů, a proto je původní matrice reprezentovatelná při kanonickém rozkladu. K takovým malinám však nedochází ve všech případech:

Příklad 8

Rozhodnutí: sestavte a vyřešte charakteristickou rovnici:

Otevříme determinant v prvním sloupci:

Další zjednodušení jsou prováděna podle zvažované metody, vyhýbající se polynomu 3. stupně:

- vlastní hodnoty.

Podívejme se na vlastní vektory:

1) Neexistují žádné problémy s kořenem:

Nebuďte překvapeni, kromě sady se používají také proměnné - zde není žádný rozdíl.

Z 3. rovnice vyjadřujeme - v 1. a 2. rovnici nahrazujeme:

Z obou rovnic vyplývá:

Nechte tedy:

2-3) Pro více hodnot dostaneme systém .

Zapíšeme matici systému a pomocí elementárních transformací ji uvedeme do postupné podoby:

Instrukce

Číslo k se nazývá vlastní číslo (číslo) matice A, pokud existuje vektor x takový, že Ax \u003d kx. (1) V tomto případě se vektor x nazývá vlastní vektor matice A, odpovídající číslu k. V prostoru R ^ n (viz obr. 1) má matice A tvar jako na obrázku.

Je nutné položit problém nalezení vektorů matice A. Nechť je vlastní vektor x dán souřadnicemi. V maticové podobě bude zapsán jako maticový sloupec, který by měl být pro snadnější představení transponovaný řádek. X \u003d (x1, x2, ..., xn) ^ T. Na základě (1), Ax-kx \u003d 0 nebo Ax-kEx \u003d 0, kde E je matice identity (ty na hlavní diagonále, všechny ostatní prvky jsou nuly). Pak (A-kE) x \u003d 0. (2)

Exprese (2) lineárních homogenních algebraických rovnic má nenulové řešení (vlastní vektory). Proto je hlavní determinant systému (2) roven nule, tj. | А-kE | \u003d 0. (3) Poslední rovnost vlastní hodnoty k se nazývá charakteristická rovnice matice A a v rozšířené formě má tvar (viz obr. 2).

Nahrazením kořene k charakteristické rovnice do systému (2) je homogenní systém lineárních rovnic s degenerovanou maticí (jeho determinant je nula). Každé nenulové řešení tohoto systému je vlastní vektor matice A odpovídající dané vlastní hodnotě k (tj. Kořen charakteristické rovnice).

Příklad. Najděte vlastní čísla a vektory matice A (viz obr. 3). Charakteristická rovnice je znázorněna na Obr. 3. Rozbalte determinant a najděte vlastní hodnoty matice, které jsou danou rovnicí (3-k) (- 1-k) -5 \u003d 0, (k-3) (k + 1) -5 \u003d 0, k ^ 2-2k -8 \u003d 0 Jeho kořeny jsou k1 \u003d 4, k2 \u003d -2

a) Vlastní vektory odpovídající k1 \u003d 4 se nacházejí prostřednictvím řešení systému (A-4kE) x \u003d 0. V tomto případě je vyžadována pouze jedna z jejích rovnic, protože determinant systému je a priori roven nule. Pokud dáme x \u003d (x1, x2) ^ T, pak první rovnice systému (1-4) x1 + x2 \u003d 0, -3x1 + x2 \u003d 0. Pokud předpokládáme, že x1 \u003d 1 (ale ne nula), pak x2 \u003d 3. Protože existuje libovolně mnoho nenulových řešení pro homogenní systém s degenerovanou maticí, celá sada vlastních vektorů odpovídá první vlastní hodnotě x \u003d C1 (1, 3), C1 \u003d konst.

b) Najděte vlastní vektory odpovídající k2 \u003d -2. Při řešení systému (A + 2kE) x \u003d 0, jeho první rovnice je (3 + 2) x1 + x2 \u003d 0,5x1 + x2 \u003d 0. Pokud dáme x1 \u003d 1, pak x2 \u003d -5. Odpovídající vlastní vektory jsou х \u003d С2 (1, 3), C2 \u003d const. Celková sada všech vlastních vektorů dané matice: x \u003d C1 (1, 3) + C2 (1, 3).

Prameny:

• Piskunov N. S. Diferenciální a integrální počet. M., 1976, - 576 str.
• najděte vlastní čísla a vektory matic

Matice, které jsou tabulkovou formou záznamu dat, se široce používají při práci se systémy lineárních rovnic. Navíc počet rovnic určuje počet řádků matice a počet proměnných určuje pořadí jejích sloupců. Výsledkem je, že řešení lineárních systémů je omezeno na operace s maticemi, z nichž jedním je hledání vlastních čísel matice. Jejich výpočet se provádí pomocí charakteristické rovnice. Vlastní hodnoty lze definovat pro čtvercovou matici řádu m.

Instrukce

Zapište daný čtverec A. Chcete-li najít jeho vlastní hodnoty, použijte charakteristickou rovnici, která vyplývá ze stavu netriviálního řešení do lineárního homogenního systému, v tomto případě reprezentovaného čtvercovou maticí. Jak vyplývá z Cramera, řešení existuje, pouze pokud je jeho determinant nulový. Můžeme tedy napsat rovnici | A - λE | \u003d 0, kde A je dané, λ jsou hledaná čísla, E je matice identity, ve které jsou všechny prvky na hlavní diagonále rovny jedné a zbytek je nula.

Proveďte násobení požadované proměnné λ identifikační maticí E stejné dimenze jako daný počáteční A. Výsledkem operace bude matice, kde hodnoty λ jsou umístěny podél hlavní diagonály, zbývající prvky zůstávají rovny nule.

Jak vložit matematické vzorce na web?

Pokud budete někdy potřebovat přidat jednu nebo dvě matematické vzorce na webovou stránku, nejjednodušší způsob je to, jak je popsáno v článku: matematické vzorce jsou snadno vloženy na web ve formě obrázků, které Wolfram Alpha automaticky generuje. Tato univerzální metoda kromě jednoduchosti pomůže zlepšit viditelnost vašich stránek ve vyhledávačích. Funguje to dlouho (a myslím, že to bude fungovat navždy), ale je morálně zastaralé.

Pokud na svém webu pravidelně používáte matematické vzorce, doporučujeme vám použít MathJax, speciální knihovnu JavaScript, která zobrazuje matematické zápisy ve webových prohlížečích pomocí značek MathML, LaTeX nebo ASCIIMathML.

Existují dva způsoby, jak začít používat MathJax: (1) s jednoduchým kódem, můžete rychle připojit skript MathJax na svůj web, který bude automaticky načten ze vzdáleného serveru ve správný čas (seznam serverů); (2) nahrajte skript MathJax ze vzdáleného serveru na váš server a připojte jej ke všem stránkám vašeho webu. Druhá metoda, která je složitější a časově náročnější, zrychlí načítání stránek vašeho webu, a pokud se z nějakého důvodu stane nadřazený server MathJax dočasně nedostupný, nebude to nijak ovlivňovat váš vlastní web. Navzdory těmto výhodám jsem si vybral první metodu, protože je jednodušší, rychlejší a nevyžaduje technické dovednosti. Postupujte podle mého příkladu a za 5 minut budete moci na svém webu používat všechny funkce MathJax.

Skript knihovny MathJax můžete připojit ze vzdáleného serveru pomocí dvou verzí kódu převzatého z hlavního serveru MathJax nebo ze stránky dokumentace:

Jedna z těchto variant kódu by měla být zkopírována a vložena do kódu vaší webové stránky, nejlépe mezi značky a nebo hned za značku ... Podle první možnosti se MathJax načítá rychleji a zpomaluje stránku méně. Druhá možnost však automaticky sleduje a načítá nejnovější verze MathJaxu. Pokud vložíte první kód, bude nutné jej pravidelně aktualizovat. Pokud vložíte druhý kód, stránky se načtou pomaleji, ale nebudete muset neustále sledovat aktualizace MathJaxu.

Nejjednodušší způsob připojení MathJaxu je v Bloggeru nebo WordPressu: na ovládacím panelu webu přidejte widget navržený pro vložení kódu JavaScript třetí strany, zkopírujte do něj první nebo druhou verzi zaváděcího kódu a umístěte widget blíže na začátek šablony (mimochodem to není vůbec nutné) protože skript MathJax je načten asynchronně). To je vše. Nyní se naučte syntaxi značek MathML, LaTeX a ASCIIMathML a jste připraveni vložit matematické vzorce do webových stránek vašeho webu.

Jakýkoli fraktál je postaven podle určitého pravidla, které se soustavně používá neomezený početkrát. Každá taková doba se nazývá iterace.

Iterační algoritmus pro konstrukci Mengerovy houby je poměrně jednoduchý: původní krychle se stranou 1 je rozdělena rovinami rovnoběžnými s jeho tvářemi na 27 stejných kostek. Jedna centrální kostka a 6 sousedních kostek jsou z ní odstraněny. Výsledkem je sada sestávající z 20 zbývajících menších kostek. Když uděláme totéž s každou z těchto kostek, dostaneme sadu, již sestávající ze 400 menších kostek. Pokračováním tohoto procesu donekonečna získáváme houbu Menger.

www.site umožňuje najít. Výpočet provede web. Během několika sekund server poskytne správné řešení. Charakteristická rovnice pro matici bude algebraický výraz nalezený pravidlem pro výpočet determinantu matice matice, zatímco hlavní úhlopříčka bude rozdíl mezi hodnotami diagonálních prvků a proměnné. Při výpočtu charakteristické rovnice pro matici online, každý prvek matice se bude násobit odpovídajícími dalšími prvky matice... Najít v režimu online možné pouze pro náměstí matice... Najděte operaci charakteristické rovnice pro matici online snižuje na výpočet algebraického součtu součinu prvků matice v důsledku nalezení determinantu matice, pouze za účelem určení charakteristické rovnice pro matici online... Tato operace zaujímá teoreticky zvláštní místo. matice, umožňuje najít vlastní hodnoty a vektory pomocí kořenů. Úkol najít charakteristické rovnice pro matici online je znásobit prvky matice s následným shrnutím těchto děl podle určitého pravidla. www.site najde charakteristická rovnice pro matici daný rozměr v režimu online... Výpočet charakteristické rovnice pro matici online pro danou dimenzi najde polynom s numerickými nebo symbolickými koeficienty, nalezený podle pravidla pro výpočet determinantu matice - jako součet produktů odpovídajících prvků matice, pouze za účelem určení charakteristické rovnice pro matici online... Nalezení polynomu v proměnné pro čtverec maticejako definice charakteristická rovnice pro matici, teoreticky běžné matice... Hodnota kořenů polynomu charakteristické rovnice pro matici online se používá ke stanovení vlastních vektorů a vlastních čísel pro matice... Navíc, pokud determinant matice bude tedy rovno nule matice charakteristická rovnice bude stále existovat, na rozdíl od opaku matice... Pro výpočet charakteristická rovnice pro matici nebo najděte několik najednou matice charakteristické rovnice, musíte strávit spoustu času a úsilí, zatímco náš server najde během několika sekund charakteristická rovnice pro matici online... V tomto případě je odpověď najít charakteristické rovnice pro matici online bude správná as dostatečnou přesností, i když čísla při hledání charakteristické rovnice pro matici online bude iracionální. Na stránce www.site symbolické záznamy v prvcích jsou povoleny matice, tj charakteristická rovnice pro matici online lze při výpočtu reprezentovat v obecné symbolické podobě charakteristická rovnice matice online... Je užitečné zkontrolovat odpověď získanou při řešení problému nalezení charakteristické rovnice pro matici onlinepomocí webu www.site... Při provádění operace výpočtu polynomu - charakteristická rovnice matice, při řešení tohoto problému je třeba být pozorný a mimořádně zaměřený. Náš web vám zase pomůže zkontrolovat vaše rozhodnutí v daném tématu online maticová charakteristická rovnice... Pokud nemáte čas na dlouhé kontroly vyřešených problémů, pak www.site bude určitě vhodným nástrojem pro kontrolu při hledání a výpočtu charakteristické rovnice pro matici online.