HOMOGÉN VONATKOZÁSOK RENDSZERE

A homogén lineáris egyenletek rendszere az alak rendszere

Nyilvánvaló, hogy ebben az esetben mivel ezekben a minősítőkben az egyik oszlop összes eleme nulla.

Mivel az ismeretleneket a képletek találják meg , akkor Δ ≠ 0 esetén a rendszernek egyedi nulla megoldása van x = y = z \u003d 0. Sok probléma esetén azonban érdekes a kérdés, hogy egy homogén rendszernek nullán kívüli megoldásokkal is rendelkezik-e.

Tétel. Ahhoz, hogy egy lineáris homogén egyenletrendszer nem nulla megoldással rendelkezzen, szükséges és elegendő, hogy Δ ≠ 0.

Tehát, ha a Δ ≠ 0 determináns, akkor a rendszernek egyedi megoldása van. Ha Δ ≠ 0, akkor a lineáris homogén egyenletek rendszerének végtelen megoldása van.

Példák.

A mátrix sajátvektorai és sajátértékei

Adjunk egy négyzetmátrixot , x - valamilyen mátrixoszlop, amelynek magassága egybeesik a mátrix sorrendjével A. .

Sok probléma esetén figyelembe kell venni az egyenletet x

ahol λ valamilyen szám. Nyilvánvaló, hogy bármely λ-nek ez az egyenlet nulla megoldással rendelkezik.

Az λ számot hívják, amelyre ez az egyenlet nem nulla megoldást tartalmaz saját jelentése mátrixok Aés x mert ilyen λ-t hívják saját vektor mátrixok A.

Keresse meg a mátrix sajátvektorát A... Amennyiben E∙X \u003d X, akkor a mátrix egyenlet átírható vagy ... Bővített formában ez az egyenlet átírható egyenes egyenletrendszerként. Igazán .

És ezért

Tehát egy homogén lineáris egyenletrendszert kaptunk a koordináták meghatározására x 1, x 2, x 3 vektor x... Annak érdekében, hogy a rendszernek nullától eltérő megoldásai legyenek, szükséges és elegendő, ha a rendszer meghatározója nullával egyenlő, azaz

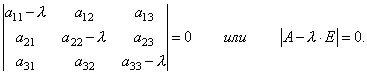
Ez egy λ-szintű 3. fokú egyenlet. Ezt hívják karakterisztikus egyenlet mátrixok A és szolgál a λ sajátértékek meghatározására.

Minden λ sajátérték egy sajátvektornak felel meg x, amelynek koordinátáit a rendszer határozza meg a megfelelő λ értéknél.

Példák.

VECTOR ALGEBRA. A VEKTOR FOGALMA

A fizika különféle ágainak tanulmányozásakor vannak olyan mennyiségek, amelyeket numerikus értékeik megadásával teljesen meg lehet határozni, például hossz, terület, tömeg, hőmérséklet stb. Az ilyen mennyiségeket skalárisnak nevezzük. Ráadásul vannak olyan mennyiségek is, amelyek meghatározásához a numerikus érték mellett meg kell ismerni a térbeli irányt is, például a testre ható erőt, a test sebességét és gyorsulását, amikor az űrben mozog, a mágneses mező erősségét az adott térbeli ponton és stb. Az ilyen mennyiségeket vektornak nevezzük.

Bemutatjuk a szigorú meghatározást.

Irányított szegmens hívjuk egy szegmenst, amelynek végeire viszonyítva tudjuk, melyik az első és melyik a második.

Vektor egy meghatározott hosszúságú, azaz egy irányított szegmensnek nevezzük, azaz egy hosszúságú szegmens, amelynek egyik határpontját kezdetként, a másik végét vesszük. Ha egy A - a vektor kezdete, B - vége, akkor a vektort egy szimbólum jelöli, emellett a vektort gyakran egy betűvel jelölik. Az ábrán a vektort egy vonalszegmens jelzi, irányát egy nyíl jelöli.

modul vagy hossz vektor a meghatározó irányszegmens hossza. Ezt a || jelzi vagy ||

Az úgynevezett nulla vektort, amelynek kezdete és vége egybeesik, vektorokra is utaljuk. Meg van jelölve. A nulla vektornak nincs határozott iránya, modulusa nulla || \u003d 0.

Vektorok és hívják kollineárisha ugyanazon a vonalon vagy párhuzamos vonalakon vannak. Sőt, ha a vektorok ugyanabban az irányban vannak, akkor ellentétesen írunk.

Az ugyanazon síkkal párhuzamos egyenes vonalakon elhelyezkedő vektorokat nevezzük egy síkban.

Két vektor, és hívják egyenlőha egyenesek, egyenlően irányítottak és egyforma hosszúak. Ebben az esetben írjon.

A vektorok egyenlőségének meghatározásából következik, hogy egy vektor átvihető magával párhuzamosan, az eredetét a tér bármely pontján elhelyezve.

például.

LINEÁRIS MŰVELETEK A SZAKASZOKKAL

1. Szorozzuk meg a vektort egy számmal.

   A λ számú vektor szorzata olyan új vektor, amely:

   Egy λ számú vektor szorzatát jelöljük.

   

   Például, "vektor", amely ugyanabba az irányba van irányítva, mint a vektor, és amelynek hossza fele a vektor hosszának.

   A bevezetett művelet a következő tulajdonságok:

2. Vektorok hozzáadása.

   Legyen és legyen két tetszőleges vektor. Vegyünk egy önkényes pontot O és összeállítunk egy vektort. Ezt követően, a lényegtől kezdve A tegye félre a vektorot. Az első vektor elejét és a második végét összekötő vektort nevezzük összeg ezeknek a vektoroknak a jelölése .

   

   A vektor-addíció megfogalmazott meghatározását nevezzük párhuzamos diagram, mivel ugyanazt a vektorösszeget kaphatjuk az alábbiak szerint. Tegye félre a pontot O vektorok és. Konstruáljunk párhuzamos diagramot ezekre a vektorokra OABS... Mivel a vektorok, akkor egy olyan vektor, amely a csúcsból húzott párhuzamos ábra átlója O, nyilvánvalóan a vektorok összege.

   

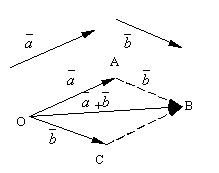
   Könnyű ellenőrizni a következőket vektor-addíciós tulajdonságok.

3. A vektorok különbsége.

   Egy adott vektorral egyirányú, egyenlő hosszúságú és ellentétes irányú vektort hívunk szemben vektor vektort, és a jelölése. Az ellenkező vektort úgy tekinthetjük, hogy a vektort megszorozzuk λ \u003d –1 számmal:

Sajátértékek (számok) és sajátvektorok.
Példák megoldásra

Légy önmagad

Mindkét egyenletből következik, hogy.

Tegyük fel, akkor: .

Ennek eredményeként: A második sajátvektor.

Ismételjük meg a megoldás fontos pontjait:

- a kapott rendszernek természetesen van általános megoldása (az egyenletek lineárisan függnek);

- úgy választjuk meg a „játékot”, hogy teljes legyen, és az első „x” koordináta teljes, pozitív és a lehető legkisebb.

- ellenőrizze, hogy az adott megoldás megfelel-e a rendszer minden egyenletének.

Válasz .

Elég sok volt a közbenső „ellenőrzési pont”, ezért az egyenlőség ellenőrzése elvileg szükségtelen kérdés.

Különböző információforrásokban a sajátvektorok koordinátáit gyakran nem oszlopokba, hanem sorokba írják, például: (és őszintén szólva szoktam magam sorba írni)... Ez a lehetőség elfogadható, de a téma fényében lineáris transzformációk műszakilag kényelmesebb használni oszlopvektorok.

Lehet, hogy a megoldás nagyon hosszúnak tűnt neked, de ez csak azért van, mert az első példát nagyon részletesen kommentáltam.

2. példa

mátrixok

Mi kiképzzük magunkat! A feladat befejezésének hozzávetőleges példája az óra végén.

Időnként további feladatra van szükség, nevezetesen:

írja a kanonikus mátrix lebontást

Ami?

Ha a mátrix sajátvektorai alakulnak ki bázis, akkor a következőképpen ábrázolható:

Hol van a mátrix, amely a sajátvektorok koordinátáiból áll, - átlós mátrix a megfelelő sajátértékekkel.

Ilyen mátrix-bomlást hívunk kánoni vagy átlós.

Vegyük figyelembe az első példa mátrixát. Saját vektorjai lineárisan független (nem collinear), és alapot képeznek. Összeállítunk egy mátrixot a koordinátáikból:

A fő átló mátrixok a megfelelő sorrendben a sajátértékek találhatók, és a többi elem nulla:
- ismét hangsúlyozom a sorrend fontosságát: "kettő" az 1. vektornak felel meg, ezért az első oszlopban található, "három" - a második vektornak.

A szokásos algoritmus szerint inverz mátrix vagy gauss-Jordan módszermegtalálja ... Nem, ez nem helyesírás! - előtte egy ritka esemény, például egy napfogyatkozás, amikor az inverz egybeesett az eredeti mátrixszal.

Még be kell írni a mátrix kanonikus lebontását:

A rendszer elemi transzformációk segítségével oldható meg, és a következő példákban ezt a módszert fogjuk használni. De itt az "iskola" módszer sokkal gyorsabban működik. A 3. egyenletből ki fogjuk fejezni: - a második egyenletben helyettesítjük:

Mivel az első koordináta nulla, egy olyan rendszert kapunk, amelynek minden egyenletéből következik.

És újra ügyeljen a lineáris függőség kötelező jelenlétére... Ha csak triviális megoldást kap , akkor vagy a sajátértéket hibásan találták meg, vagy a rendszer hibával fordította le / oldotta meg.

A kompakt koordináták értelmet adnak

sajátvektor:

És még egyszer - ellenőrizzük, hogy a megtalált megoldás megtalálható-e kielégíti a rendszer minden egyenletét... A következő bekezdésekben és az azt követő feladatokban azt javasolom, hogy ezt a kívánságot kötelező szabályként vegye figyelembe.

2) A sajátértékhez ugyanazon elv alapján a következő rendszert kapjuk:

A rendszer 2. egyenletéből az alábbiakat fejezzük ki: - helyettesítsük a harmadik egyenletben:

Mivel a "zeta" koordináta nulla, egy olyan rendszert kapunk, amelynek minden egyenletéből egy lineáris függőség következik.

Legyen

Ellenőrizzük, hogy a megoldás kielégíti a rendszer minden egyenletét.

Így a sajátvektor:

3) És végül, a rendszer megfelel a sajátértéknek:

A második egyenlet a legegyszerűbbnek tűnik, tehát kifejezzük és helyettesítjük az 1. és a 3. egyenlettel:

Minden jó - lineáris kapcsolat alakult ki, amelyet helyettesítünk a kifejezésben:

Ennek eredményeként az "x" és "y" kifejezése "z" -en történt: A gyakorlatban nem kell csak ilyen kapcsolatokat elérni, egyes esetekben sokkal kényelmesebb kifejezni mind át, mind át. Vagy akár egy "vonat" - például "X" az "igrek" és "igrek" a "z"

Tegyük fel, akkor:

Ellenőrizzük, hogy a megtalált megoldás megfelelő-e kielégíti a rendszer minden egyenletét, és írja le a harmadik sajátvektort

Válasz: sajátvektorok:

Geometriailag ezek a vektorok három különböző térbeli irányt definiálnak ("Oda és vissza")amellyel lineáris transzformáció átalakítja a nem nulla vektorokat (sajátvektorok) vele kolináris vektorokká.

Ha egy kanonikus bomlás megállapításához szükséges feltétel, akkor ez azóta lehetséges a különféle sajátértékek megfelelnek a különféle lineárisan független sajátvektoroknak. A mátrix összeállítása koordinátáik alapján az átlós mátrix nak,-nek a megfelelő sajátértékek és megtalálni inverz mátrix .

Ha feltétel szerint meg kell írni a lineáris transzformáció mátrixa sajátvektorok alapján, akkor a választ formában adjuk meg. Van különbség, és a különbség jelentős! Ehhez a mátrixhoz a „de” mátrix tartozik.

Probléma az egyszerűbb számításokkal független megoldáshoz:

5. példa

Keresse meg a mátrix által megadott lineáris transzformáció sajátvektorát

A sajátértékek megállapításakor próbálja meg ne az ügyet a 3. fokozatú polinomhoz vinni. Ezenkívül a rendszermegoldásai eltérhetnek az én megoldásaimtól - itt nincs egyértelműség; és a talált vektorok a koordinátáik arányosságáig eltérhetnek a mintavektortól. Például és. Esztétikusabb a választ formában bemutatni, de rendben van, ha a második lehetőségnél áll meg. Mindazonáltal ésszerű korlátok vannak, a változat már nem tűnik nagyon jónak.

A feladat hozzávetőleges végső mintája az óra végén.

Hogyan lehet megoldani a problémát több sajátérték esetén?

Az általános algoritmus változatlan, de megvannak a sajátosságai, és tanácsos a megoldás egyes részeit szigorúbb tudományos stílusban fenntartani:

6. példa

Keresse meg a sajátértékeket és a sajátvektorokat

Döntés

Természetesen a mesés első oszlopot tőkésítjük:

És a négyzetes trinomális faktorozása után:

Ennek eredményeként sajátértékeket kapunk, amelyek közül kettő többszörös.

Találjuk meg a sajátvektorokat:

1) A magányos katonaval az "egyszerűsített" rendszer szerint fogunk foglalkozni:

Az utolsó két egyenletből az egyenlőség jól látható, amelyet nyilvánvalóan ki kell cserélni a rendszer első egyenletébe:

Nincs jobb kombináció:
sajátvektor:

2-3) Most lőjön néhány őrzőt. Ebben az esetben kiderülhet akár kettő, akár egy sajátvektor. A gyökerek sokaságától függetlenül az értéket a determinánssal helyettesítjük ami a következőket hozza nekünk homogén lineáris egyenletrendszer:

Az Eigenvektorok pontosan vektorok
alapvető döntési rendszer

Valójában az egész lecke során csak az alapvető rendszer vektorjainak felkutatásával foglalkoztunk. Egyelőre erre a kifejezésre nem volt szükség. Egyébként azok az okos diákok, akik álcázó kabátokban csúsztatották a témát homogén egyenletekmost meg kell enni.

Az egyetlen lépés az extra sorok eltávolítása volt. Az eredmény egy-három mátrix, amelynek közepén egy formális „lépcső” található.
- alapváltozó, - szabad változók. Ezért két szabad változó létezik, az alapvető rendszer vektorai szintén kettő.

Fejezzük ki az alapváltozót szabad változók szerint:. Az "x" előtti nulla tényező lehetővé teszi, hogy abszolút bármilyen értéket vegyen fel (ami jól látható az egyenletrendszerből).

E probléma kapcsán kényelmesebb az általános megoldást nem sorban, hanem egy oszlopban írni:

A párnak saját vektorral rendelkezik:
A párnak saját vektorral rendelkezik:

jegyzet : a kifinomult olvasók felvehetik ezeket a vektorokat és szóban is - csak a rendszer elemzésével , de itt bizonyos tudásra van szükség: három változó létezik, rendszer mátrix rangsor - egység, ami azt jelenti alapvető döntési rendszer 3 - 1 \u003d 2 vektorból áll. A megtalált vektorok azonban ezen ismeretek nélkül is tökéletesen láthatók, tisztán intuitív szinten. Ebben az esetben a harmadik vektort még "szépen" írjuk:. Felhívom azonban figyelmeztetést, hogy az egyszerű kiválasztás újabb példája nem lehet, ezért a felelősségkizárás tapasztalt embereknek szól. Különben is, miért nem vesszük például a harmadik vektorba? Végül is, annak koordinátái szintén kielégítik a rendszer minden egyenletét és a vektorokat lineárisan függetlenek. Ez a lehetőség elvileg megfelelő, de "görbe", mivel az "egyéb" vektor az alaprendszer vektorjainak lineáris kombinációja.

Válasz: sajátértékek :, sajátvektorok:

Hasonló példa egy önálló megoldásra:

7. példa

Keresse meg a sajátértékeket és a sajátvektorokat

Durva példa a lecke végén történő befejezésre.

Meg kell jegyezni, hogy mind a 6., mind a 7. példában háromszor lineárisan független sajátvektorokat kapunk, ezért az eredeti mátrix reprezentatív lehet a kanonikus bomlás során. De az ilyen málna nem minden esetben fordul elő:

8. példa

Döntés: a jellemző egyenlet összeállítása és megoldása:

Az első oszlop segítségével megnyitjuk a determinánst:

A további egyszerűsítéseket a vizsgált módszer szerint hajtjuk végre, elkerülve a 3. fokú polinomot:

- sajátértékek.

Találjuk meg a sajátvektorokat:

1) A gyökérrel nincs nehézség:

Ne lepődj meg, hogy a készlet mellett változókat is használnak - itt nincs különbség.

A 3. egyenletből kifejezésre jutunk - az 1. és 2. egyenletben helyettesítjük:

Mindkét egyenletből következik:

Legyen, majd:

2-3) Több értéknél kapjuk meg a rendszert .

Leírjuk a rendszer mátrixát, és elemi átalakítások segítségével lépcsőzetes formába állítjuk:

Utasítás

A k számot az A mátrix sajátértékének (számának) nevezzük, ha van olyan vektor x, hogy Ax \u003d kx. (1) Ebben az esetben az x vektort az A mátrix sajátvektorának nevezzük, amely k számnak felel meg. Az R ^ n térben (lásd az 1. ábrát) az A mátrix az ábrán látható formájú.

Fel kell vetni az A mátrix vektorának megtalálásának problémáját. Legyen x sajátvektor koordinátákkal megadva. Mátrix formában mátrix oszlopként kell írni, amelyet az egyszerűség kedvéért átültetett sorként kell ábrázolni. X \u003d (x1, x2,…, xn) ^ T. Az (1) alapján Ax-kx \u003d 0 vagy Ax-kEx \u003d 0, ahol E az identitási mátrix (a fő átlóson, az összes többi elem nulla). Ezután (A-kE) x \u003d 0. (2)

A lineáris homogén algebrai egyenletek kifejezésének (2) nem nulla megoldása van (sajátvektor). Ezért a (2) rendszer fő meghatározója nulla, azaz | А-kE | \u003d 0. (3) A k sajátérték utolsó egyenlőségét az A mátrix jellemző egyenletének nevezzük, és kibővített formában a következő formájú (lásd 2. ábra).

A karakterisztikus egyenlet gyökerének a (2) rendszerbe történő felváltásával egy lineáris egyenletek homogén rendszerét degenerált mátrixszal (meghatározó értéke nulla). A rendszer minden nem nulla megoldása az A mátrix sajátvektora, amely egy adott k sajátértékre (vagyis a karakterisztikus egyenlet gyökerére) vonatkozik.

Példa. Keresse meg az A mátrix sajátértékét és vektorát (lásd 3. ábra). A karakterisztikus egyenletet a 2. ábra mutatja. 3. Bontsa ki a determinánst és keresse meg a mátrix sajátértékeit, amelyek az adott egyenlet (3-k) (- 1-k) -5 \u003d 0, (k-3) (k + 1) -5 \u003d 0, k ^ 2-2k -8 \u003d 0 Gyökerei k1 \u003d 4, k2 \u003d -2

a) A k1 \u003d 4-nek megfelelő sajátvektorokat a rendszer (A-4kE) x \u003d 0 megoldásával találjuk meg. Ebben az esetben csak az egyik egyenletére van szükség, mivel a rendszer meghatározója a priori nullával egyenlő. Ha x \u003d (x1, x2) ^ T-t adunk, akkor az (1-4) rendszer első egyenlete x1 + x2 \u003d 0, -3x1 + x2 \u003d 0. Ha feltételezzük, hogy x1 \u003d 1 (de nem nulla), akkor x2 \u003d 3. Mivel tetszőlegesen sok nem nulla megoldás létezik egy degenerált mátrixú homogén rendszerre, az x \u003d C1 (1, 3) első sajátértékhez tartozó teljes sajátvektorkészlet, C1 \u003d const.

b) Keresse meg a sajátvektorokat, amelyek megfelelnek a k2 \u003d -2-nek. A rendszer (A + 2kE) x \u003d 0 megoldásakor az első egyenlete (3 + 2) x1 + x2 \u003d 0,5x1 + x2 \u003d 0. Ha x1 \u003d 1-et adunk, akkor x2 \u003d -5. A megfelelő sajátvektorok х \u003d С2 (1, 3), C2 \u003d állandó. Egy adott mátrix összes sajátvektorának összessége: x \u003d C1 (1, 3) + C2 (1, 3).

Forrás:

• Piskunov N.S. Differenciál és integrált számítás. M., 1976, - 576 p.
• megtalálja a mátrixok sajátértékét és vektorát

A mátrixokat, amelyek az adatrögzítés táblázatos formája, széles körben használják lineáris egyenletrendszerekkel való munka során. Ezenkívül az egyenletek száma meghatározza a mátrix sorainak számát, a változók száma pedig az oszlopok sorrendjét. Ennek eredményeként a lineáris rendszerek megoldása mátrixokon végzett műveletekre redukálódik, amelyek egyike a mátrix sajátértékeinek keresése. Számításukat a jellemző egyenlet felhasználásával hajtják végre. A sajátértékek meghatározhatók m sorrendű négyzetes mátrixra.

Utasítás

Írja le egy adott A négyzetet. A sajátértékének meghatározásához használja a jellemző egyenletet, amely a nem-triviális megoldás feltételétől egy lineáris homogén rendszerhez vezet, amelyet ebben az esetben egy négyzetmátrix képvisel. A Cramer-ből következik, hogy megoldás csak akkor létezik, ha annak determinánsa nulla. Így megírhatjuk a | egyenletet A - λE | \u003d 0, ahol A egy adott, λ a keresett szám, E az azonossági mátrix, amelyben a fõ átló összes eleme egyenlő, a többi nulla.

Végezzük el a kívánt λ változó szorzását az adott A kezdettel megegyező méretű E azonosító mátrixszal. A művelet eredményeként mátrix lesz, ahol λ értékei a fő átlós mentén helyezkednek el, a többi elem nulla.

Hogyan lehet beágyazni matematikai képleteket egy weboldalra?

Ha valaha hozzá kell adnia egy vagy két matematikai képletet egy weboldalhoz, akkor ezt a legegyszerűbben a cikkben leírt módon hajthatja végre: a matematikai képleteket könnyen beilleszthetik a webhelybe olyan képek formájában, amelyeket a Wolfram Alpha automatikusan generál. Az egyszerűség mellett ez a sokoldalú módszer javítja webhelye láthatóságát a keresőmotorokban is. Régóta működik (és azt hiszem, örökké fog működni), de erkölcsileg már elavult.

Ha rendszeresen használ matematikai képleteket webhelyén, akkor azt javaslom, hogy használja a MathJax-ot, egy speciális JavaScript könyvtárat, amely a MathML, LaTeX vagy ASCIIMathML jelöléssel használja a böngészők matematikai jelöléseit.

Kétféle módon lehet elkezdeni a MathJax használatát: (1) egy egyszerű kód használatával gyorsan csatlakoztathat egy MathJax szkriptet a webhelyéhez, amelyet automatikusan betölt a távoli szerverről a megfelelő időben (kiszolgálói lista); (2) töltse fel a MathJax szkriptet egy távoli szerverről a szerverre, és csatlakoztassa a webhely összes oldalához. A második, bonyolultabb és időigényesebb módszer felgyorsítja a webhely oldalai betöltését, és ha a szülő MathJax szerver valamilyen okból ideiglenesen nem elérhető, ez semmilyen módon nem érinti a saját webhelyét. Ezen előnyök ellenére az első módszert választottam, mivel egyszerűbb, gyorsabb és nem igényel műszaki ismereteket. Kövesse a példát, és 5 perc múlva képes lesz használni a webhely összes MathJax szolgáltatását.

A MathJax könyvtár parancsfájlját távoli kiszolgálótól összekapcsolhatja a MathJax fő webhelyéről vagy a dokumentációs oldalból vett kód két verziójával:

Ezeknek a kódváltozatoknak az egyikét át kell másolni és beilleszteni a weboldal kódjába, lehetőleg címkék között és vagy közvetlenül a címke után ... Az első lehetőség szerint a MathJax gyorsabban töltődik be, és kevésbé lassítja az oldalt. De a második lehetőség automatikusan követi és betölti a MathJax legújabb verzióit. Ha beilleszti az első kódot, akkor azt rendszeresen frissíteni kell. Ha beilleszti a második kódot, az oldalak lassabban töltődnek be, de nem kell folyamatosan ellenőriznie a MathJax frissítéseit.

A MathJax csatlakoztatásának legegyszerűbb módja a Blogger vagy a WordPress: a webhely irányítópultjába adjon hozzá egy widget, amely harmadik féltől származó JavaScript kód beillesztésére szolgál, másolja bele a fenti letöltési kód első vagy második verzióját, és helyezze a widget közelebb a sablon elejéhez (egyébként erre nincs szükség) mert a MathJax szkript aszinkron módon van betöltve). Ez minden. Most tanulja meg a MathML, LaTeX és ASCIIMathML jelölési szintaxist, és készen áll arra, hogy a matematikai képleteket beágyazza webhelye weblapjaira.

Bármelyik fraktált egy bizonyos szabály szerint építik fel, amelyet korlátlan számú alkalommal alkalmaznak egymásra. Minden ilyen időt iterációnak hívunk.

A Menger szivacs szerkesztésének iteratív algoritmusa meglehetősen egyszerű: az eredeti 1. oldali kocka felületével párhuzamos síkokkal 27 egyenlő kockára van osztva. Az egyik központi kocka és 6 szomszédos kocka eltávolításra kerül. Kiderül, hogy egy készlet 20 megmaradt kisebb kockából áll. Ha ugyanezt hajtjuk végre ezen kockák mindegyikével, akkor kapunk egy készletet, amely már 400 kisebb kockából áll. Ha ezt a folyamatot végtelenül folytatjuk, kapunk egy Menger szivacsot.

www.site segítségével megtalálhatja. A webhely elvégzi a számítást. Néhány másodperc alatt a szerver megadja a helyes megoldást. A mátrix jellemző egyenlete egy algebrai kifejezés, amelyet a determináns kiszámításának szabálya talál mátrixok mátrixok, míg a fő átló a különbség az átlós elemek és a változó között. Számításkor a mátrix jellemző egyenletének az interneten történő megadása, minden elem mátrixok meg fog szorozni a megfelelő többi elemmel mátrixok... Keressen üzemmódban online csak négyzet alakú mátrixok... Keresse meg a műveletet a mátrix jellemző egyenletének az interneten történő megadása az elemek szorzata algebrai összegének kiszámításához redukálódik mátrixok a determináns megtalálásának eredményeként mátrixok, csak a meghatározás céljából a mátrix jellemző egyenletének az interneten történő megadása... Ez a művelet az elméletben különleges helyet foglal el. mátrixok, lehetővé teszi a sajátértékek és vektorok megtalálását a gyökerek segítségével. A találás feladata a mátrix jellemző egyenletének az interneten történő megadása az elemek szorzata mátrixok ezeknek a műveknek a későbbi összesítésével egy bizonyos szabálynak megfelelően. www.site leletek karakterisztikus egyenlet adott dimenzió az üzemmódban online... Számítás a mátrix jellemző egyenletének az interneten történő megadása egy adott dimenzió esetében ez egy olyan polinom keresése numerikus vagy szimbolikus együtthatókkal, amelyet a determináns kiszámításának szabálya alapján találunk mátrixok - a megfelelő elemek szorzataként mátrixok, csak a meghatározás céljából a mátrix jellemző egyenletének az interneten történő megadása... Polinom keresése egy négyzet változójában mátrixokmint meghatározás a mátrix jellemző egyenlete, elméletileg általános mátrixok... A polinom gyökereinek értéke a mátrix jellemző egyenletének az interneten történő megadása a sajátvektorok és a sajátértékek meghatározására szolgál mátrixok... Sőt, ha a meghatározó mátrixok akkor nullával egyenlő mátrix karakterisztikus egyenlet továbbra is létezik, ellentétben a fordítottal mátrixok... A számítás érdekében karakterisztikus egyenlet vagy keressen egyszerre többet mátrix karakterisztikus egyenletek, sok időt és erőfeszítést kell költenie, amíg szerverünk megtalálja az online mátrix jellemző egyenlete... Sőt, a válasz az, hogy megtaláljuk a mátrix jellemző egyenletének az interneten történő megadása helyesek és kellő pontossággal, még akkor is, ha a számok megtaláláskor a mátrix jellemző egyenletének az interneten történő megadása irracionális lesz. Az oldalon www.site karakterbevitel megengedett az elemekben mátrixok, vagyis az online mátrix jellemző egyenlete ábrázolható általános szimbolikus formában a számítás során az online mátrix jellemző egyenlete... Hasznos ellenőrizni a kapott választ, amikor megoldja a találási problémát a mátrix jellemző egyenletének az interneten történő megadásaaz oldal használatával www.site... A polinom kiszámításának végrehajtásakor - a mátrix jellemző egyenlete, ennek a problémának a megoldásakor figyelmesnek és rendkívül koncentráltnak kell lennie. Webhelyünk viszont segít ellenőrizni a témával kapcsolatos döntését online mátrix karakterisztikus egyenlet... Ha nincs időd a megoldott problémák hosszú ellenőrzésére, akkor www.site minden bizonnyal kényelmes eszköz a keresés és a számítás ellenőrzéséhez a mátrix jellemző egyenletének az interneten történő megadása.